
分析 (1)根据一元二次方程x2+(2m-3)x+m2=0有两个实数根得到△=(2m-3)2-4m2=-12m+9≥0,求出m的取值范围;
(2)首先根据根与系数关系的关系得到x1+x2=3-2m,x1•x2=m2,然后得到x${\;}_{1}^{2}$+3x1x2+x${\;}_{2}^{2}$=(3-2m)2-2m2+3m2=2m2-12m+9=5m2-12m+9=4,求出m的值即可.
解答 解:(1)∵关于x的一元二次方程x2+(2m-3)x+m2=0有两个实数根x1和x2,
∴△≥0,
∴△=(2m-3)2-4m2=-12m+9≥0,
∴m≤$\frac{3}{4}$,
(2)由题意得x1+x2=3-2m,x1•x2=m2,
∵(x1+x2)2-2x1•x2=x${\;}_{1}^{2}$+x${\;}_{2}^{2}$,
∴x${\;}_{1}^{2}$+3x1x2+x${\;}_{2}^{2}$=(3-2m)2-2m2+3m2=2m2-12m+9=5m2-12m+9,
∵x${\;}_{1}^{2}$+3x1x2+x${\;}_{2}^{2}$=5,
∴5m2-12m+9=5,
∴(5m-2)(m-2)=0,
∴m1=2,m2=$\frac{2}{5}$,
∵由(1)知道m≤$\frac{3}{4}$,
∴m=$\frac{2}{5}$.
点评 本题考查了根的判别式与根与系数的关系的知识,解答本题的关键是把x${\;}_{1}^{2}$+3x1x2+x${\;}_{2}^{2}$=5转化为关于m的一元二次方程,此题还要掌握一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△≥0,方程有两个的实数根.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
| 月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3x+2 | B. | y=3x-2 | C. | y=3x+6 | D. | y=3x-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
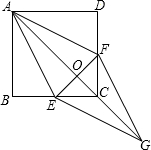 如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com