
分析 (1)根据二次根式的性质,进行化简,即可解答,由此解答.
(2)根据(1)的解答,得出规律;
(3)判断π-4<0,$\sqrt{2}$-3<0,即可解答;
(4)分两种情况,进行解答;
(5)因为2<x<3,所以x-2>0,x-3<0,即可解答.
解答 解:(1)①$\sqrt{(-2)^{2}}=\sqrt{{2}^{2}}=2$,②$\sqrt{(-0.1)^{2}}=\sqrt{0.{1}^{2}}=0.1$,
③$\sqrt{(-\frac{2}{5})^{2}}=\sqrt{(\frac{2}{5})^{2}}=\frac{2}{5}$,④$\sqrt{(-2\frac{1}{2})^{2}}=\sqrt{(2\frac{1}{2})^{2}}=2\frac{1}{2}$,
故答案为:2;0.1;$\frac{2}{5}$;$2\frac{1}{2}$.
(2)观察(1)中的结果并被开方数的底数之间的关系:我们可以得出:$\sqrt{{a}^{2}}=-a$(a<0);
故答案为:-a.
(3)①$\sqrt{(π-4)^{2}}=4-π$,②$\sqrt{(\sqrt{2}-3)^{2}}=3-\sqrt{2}$,
故答案为:4-π;3-$\sqrt{2}$.
(4)$\sqrt{{a}^{2}}=|a|=\left\{\begin{array}{l}{a(a≥0)}\\{-a(a<0)}\end{array}\right.$;
(5)∵2<x<3,
∴x-2>0,x-3<0,
$\sqrt{{x}^{2}}+\sqrt{(x-2)^{2}}-\sqrt{{x}^{2}-6x+9}$
=x+x-2-$\sqrt{(x-3)^{2}}$
=2x-2-(3-x)
=2x-2-3+x
=3x-5.
点评 本题考查了二次根式的性质与化简,解决本题的关键是熟记二次根式的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
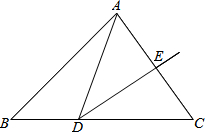 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )
如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )| A. | 13cm | B. | 15cm | C. | 17cm | D. | 19cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 35 | B. | 36 | C. | 37 | D. | 38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
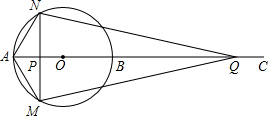 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
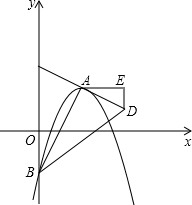 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{4}$(x-m)2+$\frac{1}{4}$m2-m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com