练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
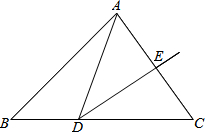
    9．如图，在△ABC中，AC的垂直平分线交BC于点D，交AC于点E，连接AD．若△ABC的周长是17cm，AE=2cm，则△ABD的周长是（　　）
    A．13cmB．15cmC．17cmD．19cm

    分析 由DE是AC的垂直平分线，根据线段垂直平分线的性质，可得AD=CD，AC=2AE=2×2=4（cm），继而可得△ABD的周长=AB+BC，又由△ABC的周长是17cm，即可求得AB+BC=13cm．

    解答 解：∵DE是AC的垂直平分线，
    ∴AD=CD，AC=2AE=2×2=4（cm），
    ∵△ABC的周长是17cm，
    ∴AB+BC=17-4=13（cm），
    ∴△ABD的周长为：AB+BD+AD=AB+BD+CD=AB+BC=13cm．
    故选A．

    点评 此题考查了线段垂直平分线的性质．注意垂直平分线上任意一点，到线段两端点的距离相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年江苏省八年级下学期第一次月考数学试卷（解析版） 题型：单选题

    的运算结果正确的是（　　）

    A. B. C. D. a+b

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

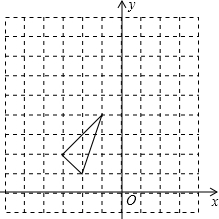    20．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，2）．
    （1）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点坐标；
    （2）若点D（a，b）在线段AB上，请直接写出经过（1）的变化后点D的对应点D1坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．将一个边长为0.1cm的正方形的边分别10等分，再连接各对边的对应分点，这些连线将原正方形分成100个完全相同的小正方形，选取其中的一个小正方形，再按照上面的方法，将这个小正方形分成100个小正方形，再选取其中的一个小正方形同样按照上面的方法，将这个小正方形分成100个小正方形，作最后得到的一个小正方形的内切圆，这个圆的半径用科学记数法表示为5×10-5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本，这个班的学生有45人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）请计算：
    ①$\sqrt{（-2）^{2}}=\sqrt{（\;\;\;\;）}$=2 ②$\sqrt{（-0.1）^{2}}=\sqrt{（\;\;\;\;）}$=0.1
    ③$\sqrt{（-\frac{2}{5}）^{2}}=\sqrt{（\;\;\;\;）}$=$\frac{2}{5}$④$\sqrt{（-2\frac{1}{2}）^{2}}=\sqrt{（\;\;\;\;）}$=2$\frac{1}{2}$
    （2）观察（1）中的结果并被开方数的底数之间的关系：我们可以得出：$\sqrt{{a}^{2}}$=-a（a＜0）
    （3）请直接填空：①$\sqrt{（π-4）^{2}}$=4-π ②$\sqrt{（\sqrt{2}-3）^{2}}$
    （4）结合课文中的公式，$\sqrt{{a}^{2}}$=a（a≥0）我们可以把二次根式$\sqrt{{a}^{2}}$化简为：$\sqrt{{a}^{2}}$=|a|=$\left\{\begin{array}{l}{a，（）}\\{-a，（）}\end{array}\right.$
    （5）化简：$\sqrt{{x}^{2}}+\sqrt{（x-2）^{2}}-\sqrt{{x}^{2}-6x+9}（2＜x＜3）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

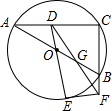    1．如图，⊙O是△ABC的外接圆，AB为直径，过点O作OD∥BC，交AC于点D．
    （1）求∠ADO的度数；
    （2）延长DO交⊙O于点E，过E作⊙O的切线，交CB延长线于点F，连接DF交OB于点G．
    ①试判断四边形CDEF的形状，并说明理由；
    ②若BG=2，AD=3，求四边形CDEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

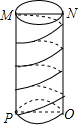    16．如图，MN是圆柱底面的直径，MP是圆柱的高，在圆柱的侧面上，过点M，P有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿MP剪开，所得的侧面展开图可以是（　　）
    A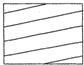．B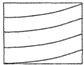．C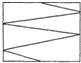．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

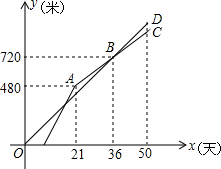    16．甲、乙两个工程队共同开凿一条隧道，甲对按一定的工作效率先施工，一段时间后，乙队从隧道的另一端按一定的工作效率加入施工，中途乙队遇到碎石层，工作效率降低，当乙队完成碎石层时恰好隧道被打通，此时甲队工作了50天．设甲、乙两队各自开凿隧道的长度为y（米），甲对的工作时间为x（天），y与x之间的函数图象如图所示．
    （1）求甲队的工作效率；
    （2）求乙队在碎石层施工时y与x之间的函数关系式；
    （3）求这条隧道的总长度．

    查看答案和解析>>

    同步练习册答案