
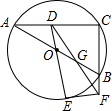
 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OD∥BC,交AC于点D.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OD∥BC,交AC于点D.分析 (1)由圆周角和平行线的性质求出结论.
(2)根据矩形的判定定理得出结论.
(3)根据三角形相似和勾股定理得到方程,联立方程组求出CF的长度,即可求出矩形的面积.
解答 解:(1)∵AB为⊙O直径,
∴∠C=90°,
∵OD∥BC,
∴∠ADO=∠C=90°;
(2)∵EF是⊙O的切线,AB为⊙O直径,
∴∠DEF=90°,
由(1)知∠ADO=∠C=90°,
∴∠ADO=∠C=∠DEF=90°,
∴四边形CDEF是矩形;
(3)∵四边形DEFC是矩形,
∴ED⊥AC,DE=CF,
∴CD=AD=3,
设DE=CF=y,⊙O的半径=r,
∵OD∥CF,
∴$\frac{OD}{BF}$=$\frac{OG}{BG}$,
∴$\frac{y-r}{y-2(y-r)}$=$\frac{r-2}{2}$,
在Rt△ADO中,32+(y-r)2=r2,
解$\left\{\begin{array}{l}{\frac{y-r}{y-2(y-r)}=\frac{r-2}{2}}\\{{3}^{2}{+(y-r)}^{2}{=r}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{y=\frac{9}{2}}\\{r=\frac{13}{4}}\end{array}\right.$,
∴S四边形DEFC=$\frac{9}{2}$×3=$\frac{27}{2}$.
点评 本题考查了切线的性质,矩形的判定和性质,圆周角定理,相似三角形的判定和性质,找准相似三角形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
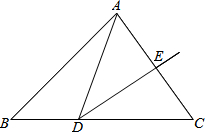 如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )
如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD.若△ABC的周长是17cm,AE=2cm,则△ABD的周长是( )| A. | 13cm | B. | 15cm | C. | 17cm | D. | 19cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量/m3 | 水费/元 |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
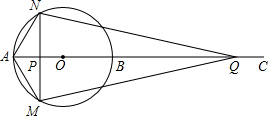 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:判断题
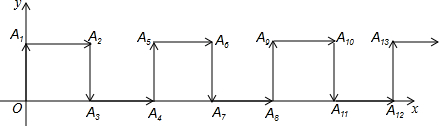
已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标.
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
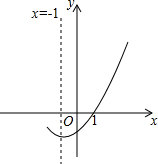 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com