
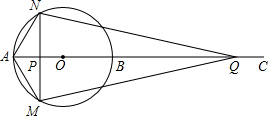
 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.分析 (1)AP=t,CQ=t,则PQ=5-2t,由于NM⊥AB,根据垂径定理得PM=PN,根据菱形的判定方法,当PA=PQ时,四边形AMQN为菱形,即t=5-2t,然后解一元一次方程可求t的值;根据切线的判定定理,当∠ONQ=90°时,NQ与⊙O相切,如图,此时OP=t-1,OQ=AC-OA-QC=4-t,再证明Rt△ONP∽Rt△OQN,利用相似比可得t2-5t+5=0,然后解一元二次方程可得到t的值;
(2)当四边形AMQN为正方形.则∠MAN=90°,根据圆周角定理得到MN为⊙O的直径,而∠MQN=90°,又可判断AQ为直径,于是得到点P在圆心,所以t=AP=1,CQ=t=1,则可得到此时AC=AQ+CQ=3.
解答 解:(1)AP=t,CQ=t,则PQ=5-2t,
∵NM⊥AB,
∴PM=PN,
∴当PA=PQ时,四边形AMQN为菱形,即t=5-2t,解得t=$\frac{5}{3}$;
当∠ONQ=90°时,NQ与⊙O相切,如图,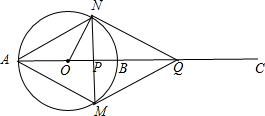
OP=t-1,OQ=AC-OA-QC=5-1-t=4-t,
∵∠NOP=∠QON,
∴Rt△ONP∽Rt△OQN,
∴$\frac{ON}{OQ}$=$\frac{OP}{ON}$,即$\frac{1}{4-t}$=$\frac{1-t}{1}$,
整理得t2-5t+5=0,解得t1=$\frac{5-\sqrt{5}}{2}$,t2=$\frac{5+\sqrt{5}}{2}$(1≤t≤2.5,故舍去),
即当t=$\frac{5-\sqrt{5}}{2}$时,NQ与⊙O相切;
故答案为$\frac{5}{3}$,$\frac{5-\sqrt{5}}{2}$;
(2)当AC的长为3时,存在t=1,使四边形AMQN为正方形.理由如下:
∵四边形AMQN为正方形.
∴∠MAN=90°,
∴MN为⊙O的直径,
而∠MQN=90°,
∴点Q在⊙O上,
∴AQ为直径,
∴点P在圆心,
∴MN=AQ=2,AP=1,
∴t=AP=1,CQ=t=1,
∴AC=AQ+CQ=2+1=3.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了菱形和正方形的判定.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
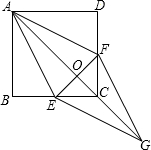 如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
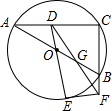 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OD∥BC,交AC于点D.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OD∥BC,交AC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
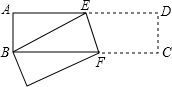 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与D重合,折痕为EF,则BE的长为( )
已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与D重合,折痕为EF,则BE的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
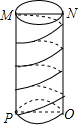 如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )
如图,MN是圆柱底面的直径,MP是圆柱的高,在圆柱的侧面上,过点M,P有一条绕了四周的路径最短的金属丝,现将圆柱侧面沿MP剪开,所得的侧面展开图可以是( )| A. | 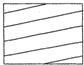 | B. | 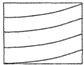 | C. | 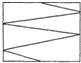 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com