
���� ��1����ͶӰ��ÿ̨xԪ������ÿ̨yԪ�������������������������⼴�ɣ�
��2�������Ϊą����ͶӰ��Ϊ��500-a��̨�����ݵ��Ե�̨��������ͶӰ��̨����4�����г�һ�κ���������ɣ�
��� �⣺��1���蹺��һ̨�ʼDZ�������xԪ������1̨ͶӰ����yԪ��
���Եõ������飺$\left\{\begin{array}{l}{y-3x=3000}\\{5x+4y=80000}\end{array}\right.$��
��ã�x=4000��y=15000��
���Թ�����һ̨�ʼDZ�������4000Ԫ������1̨ͶӰ����15000Ԫ��
��2�������Ϊą����ͶӰ��Ϊ��500-a��̨���ܷ���ΪWԪ��
��a��4��500-a����
��a��400��
W=4000a+15000��500-a��=-11000a+7500000
��-11000��0
��W��a�����������
�൱a=400ʱ��W����Сֵ=3100000=310��Ԫ��
�𣺵��������400̨ʱ���ܷ�������Ϊ310��Ԫ��
���� ���⿼�����ж�Ԫһ�η������ʵ����������ã��ܼ�=���ۡ����������ã�һ�κ����Ľ���ʽ�����ã�һ�κ��������ʵ����ã�һԪһ�β���ʽ�����ã����ʱ��������Ľ���ʽ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=3x+2 | B�� | y=3x-2 | C�� | y=3x+6 | D�� | y=3x-6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
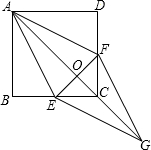 ��ͼ��������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ�AE=AF��AC��EF���ڵ�O���ӳ�AC����G��ʹ��AO=OG������EG��FG��
��ͼ��������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ�AE=AF��AC��EF���ڵ�O���ӳ�AC����G��ʹ��AO=OG������EG��FG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
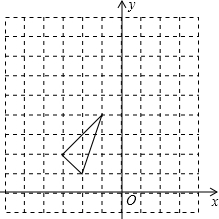 ��ͼ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��-2��1����B��-1��4����C��-3��2����
��ͼ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��-2��1����B��-1��4����C��-3��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
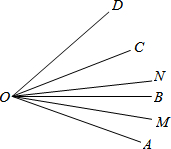 ��ͼ��OMƽ�֡�AOB��ONƽ�֡�COD������MON=42�㣬��BOC=5�㣬���AOD�Ķ�����74�㣮
��ͼ��OMƽ�֡�AOB��ONƽ�֡�COD������MON=42�㣬��BOC=5�㣬���AOD�Ķ�����74�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com