
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
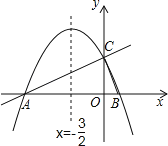
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)①(1,0);②y=![]() x2
x2![]() x+2.(2)当m=﹣2时,△PAC的面积有最大值是4,此时P(﹣2,3).(3)存在M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18),使得以点A、M、N为顶点的三角形与△ABC相似.
x+2.(2)当m=﹣2时,△PAC的面积有最大值是4,此时P(﹣2,3).(3)存在M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18),使得以点A、M、N为顶点的三角形与△ABC相似.
【解析】
试题分析:(1)①先求的直线y=![]() x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;
x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;
(2)设点P、Q的横坐标为m,分别求得点P、Q的纵坐标,从而可得到线段PQ=![]() m2﹣2m,然后利用三角形的面积公式可求得S△PAC=
m2﹣2m,然后利用三角形的面积公式可求得S△PAC=![]() ×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;
×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;
(3)首先可证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC; ④当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
解:(1)①y=![]() 当x=0时,y=2,当y=0时,x=﹣4,
当x=0时,y=2,当y=0时,x=﹣4,
∴C(0,2),A(﹣4,0),
由抛物线的对称性可知:点A与点B关于x=﹣![]() 对称,
对称,
∴点B的坐标为(1,0).
②∵抛物线y=ax2+bx+c过A(﹣4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x﹣1),
又∵抛物线过点C(0,2),
∴2=﹣4a
∴a=![]()
∴y=![]() x2
x2![]() x+2.
x+2.
(2)设P(m,![]() m2
m2![]() m+2).
m+2).
过点P作PQ⊥x轴交AC于点Q,
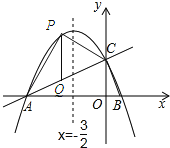
∴Q(m,![]() m+2),
m+2),
∴PQ=![]() m2
m2![]() m+2﹣(
m+2﹣(![]() m+2)
m+2)
=![]() m2﹣2m,
m2﹣2m,
∵S△PAC=![]() ×PQ×4,
×PQ×4,
=2PQ=﹣m2﹣4m=﹣(m+2)2+4,
∴当m=﹣2时,△PAC的面积有最大值是4,
此时P(﹣2,3).
(3)在Rt△AOC中,tan∠CAO=![]() 在Rt△BOC中,tan∠BCO=
在Rt△BOC中,tan∠BCO=![]() ,
,
∴∠CAO=∠BCO,
∵∠BCO+∠OBC=90°,
∴∠CAO+∠OBC=90°,
∴∠ACB=90°,
∴△ABC∽△ACO∽△CBO,
如下图:
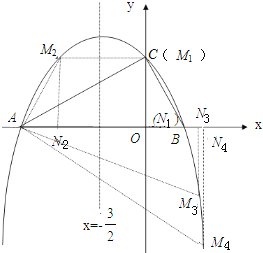
①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;
②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;
③当点M在第四象限时,设M(n,![]() n2
n2![]() n+2),则N(n,0)
n+2),则N(n,0)
∴MN=![]() n2+
n2+![]() n﹣2,AN=n+4
n﹣2,AN=n+4
当![]() 时,MN=
时,MN=![]() AN,即
AN,即![]() n2+
n2+![]() n﹣2=
n﹣2=![]() (n+4)
(n+4)
整理得:n2+2n﹣8=0
解得:n1=﹣4(舍),n2=2
∴M(2,﹣3);
当![]() 时,MN=2AN,即
时,MN=2AN,即![]() n2+
n2+![]() n﹣2=2(n+4),
n﹣2=2(n+4),
整理得:n2﹣n﹣20=0
解得:n1=﹣4(舍),n2=5,
∴M(5,﹣18).
综上所述:存在M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18),使得以点A、M、N为顶点的三角形与△ABC相似.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
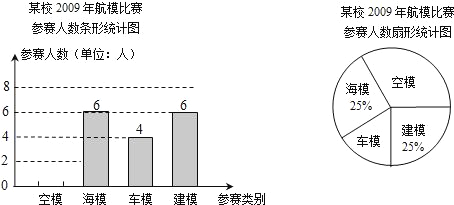
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
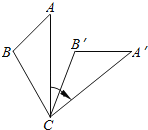
A.110° B.80° C.40° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com