
【题目】已知抛物线![]() 过点
过点![]() ,
,![]() ,
,![]() .
.
(1)求此抛物线的解析式;
(2)若点![]() 是该抛物线第三象限的任意一点,求四边形
是该抛物线第三象限的任意一点,求四边形![]() 的最大面积;
的最大面积;
(3)若点![]() 在
在![]() 轴上,点
轴上,点![]() 为该抛物线的顶点,且
为该抛物线的顶点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(0,
;(3)(0,![]() )或(0,-
)或(0,-![]() )
)
【解析】
(1)把![]() ,
,![]() ,
,![]() 代入解析式,解方程组求出a、b、c,即可求出函数解析式;
代入解析式,解方程组求出a、b、c,即可求出函数解析式;
(2)如图1,过点H作HM⊥AB于M,设点H的坐标为:![]() ,根据S四边形OCHA=S△AHM+S梯形OCHM=
,根据S四边形OCHA=S△AHM+S梯形OCHM=![]() 代入整理,得出
代入整理,得出![]() S四边形OCHA=
S四边形OCHA=![]() ,再求出二次函数的最大值即可;
,再求出二次函数的最大值即可;
(3)假设对称轴与x轴交于N点,根据已知条件可知,NG=NA,以N为圆心NG为半径作圆,与y轴的交点就是Q,再求出它的坐标,然后证明符合条件Q有且只有这两点,即可得出答案.
解:(1)∵抛物线![]() 过点
过点![]() ,
,![]() ,
,![]()
∴
解得: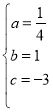
∴抛物线的解析式为:![]()
(2)如图1,过点H作HM⊥AB于M,
设点H的坐标为:(m,![]() ),
),
则HM=![]() ,OM=-m,
,OM=-m,
∵点C的坐标为(0,-3),点A的坐标为(-6,0),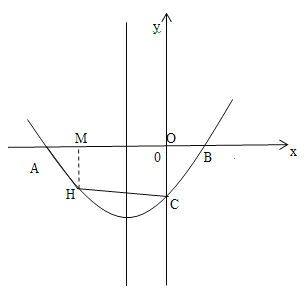
∴OA=6,OC3,
∴AM=m +6,
∴S四边形OCHA
=S△AMH+S梯形OMHC
=![]()
=![]()
=![]()
=![]()
∵![]()
∴当m=-3时,S四边形OCHA有最大值![]()
故答案为:S四边形OCHA有最大值,最大面积是;![]()
(3)如图2, ∵![]() ,
,
∴顶点坐标为(-2,-4),对称轴与x轴交于点N,
∴AN=![]()
∴NG=AN=4
以N为圆心NG为半径作圆,经过点A、B,与y轴交于点Q1、Q2,连接Q1G、Q1A、Q1N,
∵∠ANG=90°且同弧所对的圆周角等于圆心角的一半
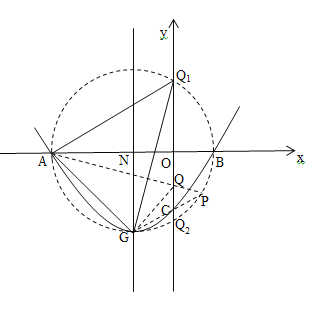
∴∠AQ1G=![]() ∠ANG=45°
∠ANG=45°
在Rt△ONQ1中,ON=2,Q1N=4
∴OQ1=![]()
∴Q1 (0,![]() )
)
由于点Q1、Q2关于 x轴对称,则Q2(0,-![]() )
)
假设在线段Q1Q2之间有点Q,如图,延长AQ交⊙N于点P,
∴∠APG=∠AQ1G=45°
而∠AQG>∠APG
∴∠AQG>45°
∴Q点不在线段Q1Q2之间;
若Q在线段Q1Q2之外时,同理可得∠AQG<45°
∴点Q不在线段Q1Q2之外;
综上所述,满足条件的点Q的坐标为:(0,![]() )或(0,-
)或(0,-![]() )
)


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 点
点![]() 是
是![]() 的平分线与抛物线的交点.
的平分线与抛物线的交点.
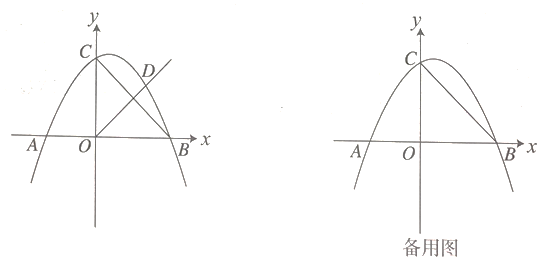
![]() 求抛物线的解析式及点
求抛物线的解析式及点![]() 的坐标;
的坐标;
![]() 点
点![]() 在平面直角坐标系内,且以
在平面直角坐标系内,且以![]() 点为顶点的四边形是平行四边形,请直接写出满足条件的点
点为顶点的四边形是平行四边形,请直接写出满足条件的点![]() 的坐标.
的坐标.
![]() 若点
若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,且点
上方抛物线上的一个动点,且点![]() 的横坐标为
的横坐标为![]() 请写出
请写出![]() 的面积
的面积![]() 与
与![]() 之间的关系式,并求出
之间的关系式,并求出![]() 为何值时,
为何值时,![]() 的面积
的面积![]() 有最大值,最大值为多少.
有最大值,最大值为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
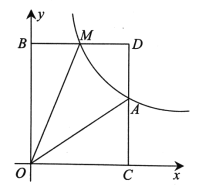
【题目】已知,如图,正比例函数y=ax的图像与反比例函数![]() 的图像交于点A(3,2).
的图像交于点A(3,2).
(1)求正比例函数与反比例函数的表达式;
(2)根据图像直接写出在第一象限内,![]() 的x的取值范围;
的x的取值范围;
(3)M(m,n)是反比例函数图像上的一个动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,证:BM=DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分,根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
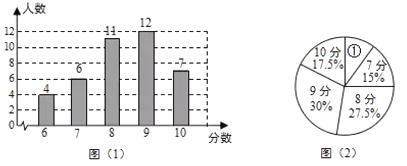
(1)①中的描述应为“6分![]() ”,其中
”,其中![]() 的值为 ;扇形①的圆心角的大小是 ;
的值为 ;扇形①的圆心角的大小是 ;
(2)求这40个样本数据的平均数、众数、中位数;
(3)若该校九年级共有360名学生,估计该校理化实验操作得满分的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
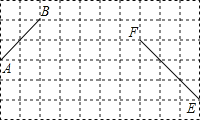
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校教学楼![]() 的后面有一栋宿舍楼
的后面有一栋宿舍楼![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,教学楼在宿舍楼的墙上留下高
时,教学楼在宿舍楼的墙上留下高![]() 的影子
的影子![]() ,而当光线与地面夹角是
,而当光线与地面夹角是![]() 时,教学楼顶
时,教学楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).则教学楼
在一条直线上).则教学楼![]() 的高度为________
的高度为________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,7月份按一定售价销售,销售额为120000元,为扩大销量,减少库存,8月份在7月份售价基础上打8折销售,结果销售量增加40件,销售额增加8000元.
(1)求该商店7月份这种商品的售价是多少元?
(2)如果该商品的进价为750元,那么该商店7月份销售这种商品的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种杂交柑橘新品种,皮薄汁多,口感细嫩,风味极佳,深受怎么喜爱,某果农种植销售过程中发现,这种柑橘的种植成本为6元/千克,日销量![]() 与销售单价
与销售单价![]() (元)之间存在一次函数关系,如图所示
(元)之间存在一次函数关系,如图所示
(1)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式
(2)该果农每天销售这种柑橘不低于60千克且不超过150千克,试求其销售单价定为多少时,除去种植成本后,每天销售利润最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com