
分析 (1)首先比较出每组两个数的平方的大小关系,然后判断出原来两个数的大小关系即可.
(2)首先比较出每组两个数的平方的大小关系,然后判断出原来两个数的大小关系即可.
解答 解:(1)${(3\sqrt{11})}^{2}=99$,${(6\sqrt{3})}^{2}=108$,
∵99<108,
∴3$\sqrt{11}$<6$\sqrt{3}$.
(2)${(-3\sqrt{7})}^{2}$=63,${(-2\sqrt{15})}^{2}$=60,
∵63>60,
∴-3$\sqrt{7}$<-2$\sqrt{15}$.
故答案为:<、<.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是比较出每组两个数的平方的大小关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:解答题
阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.

任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
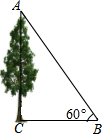 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{n}{n-m}$=-$\frac{n}{m+n}$ | B. | $\frac{n}{m-n}$=-$\frac{n}{m+n}$ | C. | $\frac{n}{n-m}$=-$\frac{-n}{m+n}$ | D. | $\frac{n}{n-m}$=-$\frac{n}{m-n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com