练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点P（x，y）满足|x+2|+（2y﹣x﹣1）2=0，则P到y轴的距离是 ．

    【答案】2
    【解析】解：∵|x+2|+（2y﹣x﹣1）2=0，
    ∴x+2=0，2y﹣x﹣1=0，
    ∴x=﹣2，
    ∴P到y轴的距离是2，
    所以答案是：2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】假期顾老师带学生乘车外出旅游，在乘车单价相同的情况下，甲、乙两位车主给出了不同的优惠方案.甲车主说“每人八折”，乙车主说“学生九折，老师免费”.李老师计算了一下，无论坐谁的车，费用都一样，则李老师带的学生为 ( )

    A. 10名 B. 9名 C. 8名 D. 17名

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（ ）

    A． B．2 C． D．10﹣5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

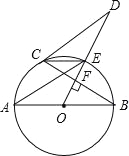
    【题目】如图，AB是⊙O的直径，OD⊥弦BC于点F，交⊙O于点E，连结CE、AE、CD，若∠AEC=∠ODC．

    （1）求证：直线CD为⊙O的切线；

    （2）若AB=5，BC=4，求线段CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】地铁1号线是重庆轨道交通线网东西方向的主干线，也是贯穿中区和沙坪坝区的重要交通通道，它的开通极大地方便了市民的出行，现某同学要从沙坪坝南开中学到两路口，他先匀速步行至沙坪坝地铁站，等了一会，然后搭乘一号线地铁直达两路口（忽略途中停靠站的时间）．在此过程中，他离南开中学的距离y与时间x的函数关系的大致图象是（　　）.
    A.
    B.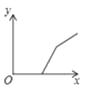
    C.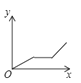
    D.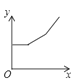

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，AB∥CD，点E为射线FG上一点．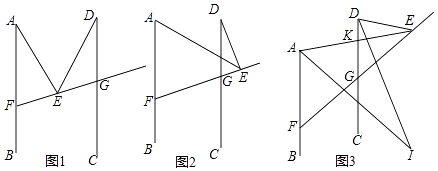
    （1）如图1，直接写出∠EAF、∠AED、∠EDG之间的数量关系；
    （2）如图2，当点E在FG延长线上时，求证：∠EAF=∠AED+∠EDG；
    （3）如图3，AI平分∠BAE，DI交AI于点I，交AE于点K，且∠EDI：∠CDI=2：1，∠AED=20°，∠I=30°，求∠EKD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若AB∥CD，AB∥EF，则CD_______EF，其理由是_______________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当五个整数从小到大排列后，其中位数是4，如果这组数据的唯一众数是6，那么这组数据可能的最大的和是_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法：①35=3×3×3×3×3；②﹣1是单项式，且它的次数为1；③若∠1=90°﹣∠2，则∠1与∠2互为余角；④对于有理数n、x、y（其中xy≠0），若 = ，则x=y．其中不正确的有（ ）
    A.3个
    B.2个
    C.1个
    D.0个

    查看答案和解析>>

    同步练习册答案