
【题目】某班数学活动小组测量吉林市“世纪之舟”的高度.他们制定了测量方案,并利用课余时间完成了实地测景,测量项目及数据如下表:
项目 | 内容 | |||
课题 | 测量吉林市“实际之舟”的高度 | |||
示意图 |
| 如图,用测角仪在 | ||
测量数据 |
|
|
| 测角仪 |
|
| 50米 | 1.5米 | |
… | … | |||
请你根据活动小组测得的数据,求世纪之舟的高![]() (结果保留小数点后一位).
(结果保留小数点后一位).
(参考数据:![]() ,
,![]() ,
,![]() )
)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
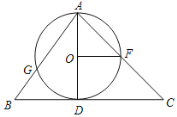
【题目】已知△ABC中,AD⊥BC,垂足为D,且AD=4,以AD为直径作圆O,交AB边于点G,交AC边于点F,如果点F恰好是![]() 的中点.
的中点.
(1)求CD的长度.
(2)当BD=3时,求BG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
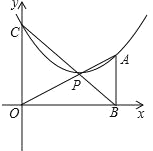
【题目】如图,A(2,1),B(2,0),C为y轴上一动点,过A,C两点的抛物线为:y=ax2+bx+n(a≠0,a≠﹣1),直线OA与直线BC交于点P,
(1)若n=1,且抛物线恰好也过P点,直接写出抛物线顶点坐标为:(_____,______)
(2)当抛物线同时经过A,C,P三点时,此时P必为该抛物线的顶点,请以n=2为例验证上述结论的正确性.
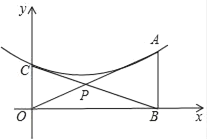
(3)若抛物线与直线BC有唯一交点C,
①求a的值;并求当C沿y轴向上运动时,其顶点同时向下运动所对应n的取值范围;
②设过B另有一直线(与BC、AB不重合),也与抛物线仅有一个交点,设为D,经探究发现:无论C在y轴上如何运动,直线CD一定经过一个确定不动点Q.请直接写出该不动点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
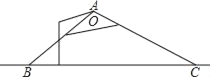
【题目】如图,一盏路灯沿灯罩边缘射出的光线与地面BC交于点B、C,测得∠ABC=45°,∠ACB=30°,且BC=20米.
(1)请用圆规和直尺画出路灯A到地面BC的距离AD;(不要求写出画法,但要保留作图痕迹)
(2)求出路灯A离地面的高度AD.(精确到0.1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
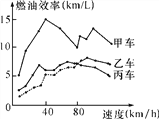
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目:初中数学 来源: 题型:
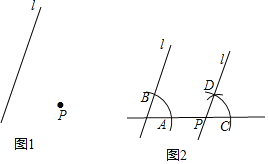
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.已知:如图1,直线l和直线l外一点P.求作:直线l的平行直线,使它经过点P.作法:如图2.(1)过点P作直线m与直线l交于点O;(2)在直线m上取一点![]() ,以点O为圆心,OA长为半径画弧,与直线l交于点B;(3)以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;(4)作直线PD.所以直线PD就是所求作的平行线.请回答:该作图的依据是______.
,以点O为圆心,OA长为半径画弧,与直线l交于点B;(3)以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;(4)作直线PD.所以直线PD就是所求作的平行线.请回答:该作图的依据是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
2014年,是全面深化改革的起步之年,是实施“十二五”规划的攻坚之年,房山区经济发展稳中有升、社会局面和谐稳定,年初确定的主要任务目标圆满完成:全年地区生产总值和固定资产投资分别为530和505亿元;区域税收完成202.8亿;城乡居民人均可支配收入分别达到3.6万元和1.9万元.
2015年,我区较好实现了“十二五”时期经济社会发展目标,开启了房山转型发展的新航程:全年地区生产总值比上年增长7%左右;固定资产投资完成530亿元;区域税收完成247亿元;公共财政预算收入完成50.02亿元;城乡居民人均可支配收入分别增长8%和10%.
2016年,发展路径不断完善,房山区全年地区生产总值完成595亿元,固定资产投资完成535亿元,超额实现预期目标,区域税收比上一年增长4.94亿元,城乡居民可支配收入分别增长8.1%和8.8%.
(摘自《房山区政府工作报告》)
根据以上材料解答下列问题:
(1)2015年,我区全年地区生产总值为______亿元.
(2)选择统计图或统计表,将我区2014~2016年全年地区生产总值、固定资产投资和区域税收表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
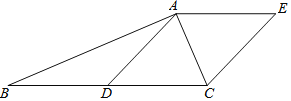
(1)求证:四边形ADCE是菱形;
(2)如果![]() ,
,![]() ,写出求菱形ADCE的面积的思路.
,写出求菱形ADCE的面积的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com