
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是 ![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP. 
(1)求证:AB是⊙O的切线.
(2)若OA=4,则 ①当 ![]() 长为时,四边形OECF是菱形;
长为时,四边形OECF是菱形;
②当 ![]() 长为时,四边形OCBP是正方形.
长为时,四边形OCBP是正方形.
【答案】
(1)解:∵在△ABO中,OA=OB,C是AB的中点,
∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
(2)![]() ;
;![]()
【解析】(2)①∵OECF为菱形, ∴OE=EC,∠EOC=∠COF.
∴OE=EC=OC.
∴∠EOC=∠COF=60°.
∴∠DOF=60°.
又∵P为弧DF的中点,
∴∠DOP=30°.
∵∠AOC=60°,∠OCA=90°,
∴OC= ![]() OA=2.
OA=2.
∴弧DP的长= ![]() =
= ![]() .
.
②∵四边形OCBP为正方形,
∴∠COB=∠POB=45°.
∴OC= ![]() OB=2
OB=2 ![]() .
.
∵P为弧DF的中点,
∴∠DOP=45°.
∴弧DP的长= ![]() =
= ![]() .
.
所以答案是:① ![]() ;②
;② ![]() .
.
(1)由等腰三角形三线合一的性质可知OC⊥AB,依据题意可知OC为⊙O的半径,故此可证明AB是⊙O的切线;(2)①由菱形的性质可知:OE=EC,∠EOC=∠COF,然后证明△OEC为等边三角形可得到∠EOC的度数,然后可求得∠DOP的度数,接下来,在△OAC中,利用特殊锐角三角函数值可求得OC的长,最后依据弧长公式求解即可;②依据正方形的性质可求得OC= ![]() ,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
【考点精析】本题主要考查了等腰三角形的性质和正方形的判定方法的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,若AB=5,AC=6,则△AMN的周长为( )
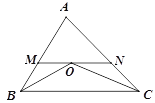
A. 7 B. 9 C. 11 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知抛物线y=ax2+bx﹣3的对称轴为x=1,与x轴分别交于A、B两点,与y轴交于点C,一次函数y=x+1经过A,且与y轴交于点D.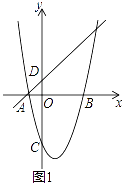
(1)求该抛物线的解析式.
(2)如图(2),点P为抛物线B、C两点间部分上的任意一点(不含B,C两点),设点P的横坐标为t,设四边形DCPB的面积为S,求出S与t的函数关系式,并确定t为何值时,S取最大值?最大值是多少?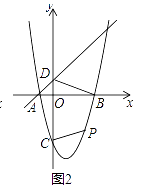
(3)如图(3),将△ODB沿直线y=x+1平移得到△O′D′B′,设O′B′与抛物线交于点E,连接ED′,若ED′恰好将△O′D′B′的面积分为1:2两部分,请直接写出此时平移的距离.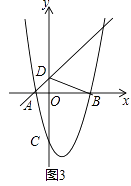
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
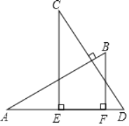
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为____.
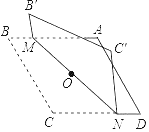
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形 ABC 中,∠A 的平分线交 BC 于点 D,过点 D 作 DE⊥AC, DF⊥AB,垂足分别为 E,F,下面四个结论:
①∠AFE=∠AEF;②AD 垂直平分 EF;③![]() ;④EF 一定平行 BC. 其中正确的是( )
;④EF 一定平行 BC. 其中正确的是( )
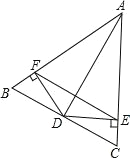
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:
组别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 | 80 |
B | 地面灰尘大,空气湿度低 | m |
C | 汽车尾气排放 | n |
D | 工厂造成的污染 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= , n= .
(2)若该市人口约有100万人,请你计算其中持D组“观点”的市民人数是多少万人?
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com