
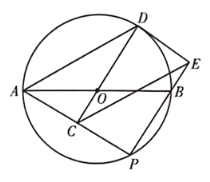
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP的中点,连接CO并延长,交⊙O于点D,连接AD,过点D作⊙O的切线,交PB的延长线于点E,连接CE.
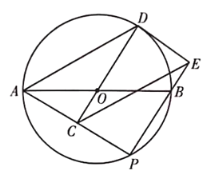
(1)求证:△DAC≌△ECP;
(2)填空:
①当∠DAP=______°时,四边形DEPC为正方形;
②在点 P的运动过程中,若⊙O的直径为10,tan∠DCE=![]() ,则AD=______.
,则AD=______.
【答案】(1)见解析;(2)①45,②![]() .
.
【解析】
(1)先由切线的性质得到∠CDE=90°,再利用垂径定理的推理得到DC⊥AP,接着根据圆周角定理得到∠APB=90°,于是可判断四边形DEPC为矩形,所以DC=EP,然后根据“SAS”判断△DAC≌△ECP;
(2)①利用四边形DEPC为矩形得到DE=PC=AC,则根据正方形的判定方法得DC=CP时,四边形DEPC为正方形,则DC=CP=AC,于是得到此时△ACD为等腰直角三角形,所以∠DAP=45°;
②先证明∠ADC=∠DCE,再在Rt△ACD中利用正切得到tan∠ADC=![]() ,则设AC=x,DC=2x,利用勾股定理得到AD=
,则设AC=x,DC=2x,利用勾股定理得到AD=![]() x,然后在Rt△AOC中利用勾股定理得到x2+(2x5)2=52,再解方程求出x即可得到AD的长.
x,然后在Rt△AOC中利用勾股定理得到x2+(2x5)2=52,再解方程求出x即可得到AD的长.
(1)证明:∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
∵点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中位线,
的中位线,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() 是圆的切线,
是圆的切线,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
(2)解:①∵四边形DEPC为矩形,
∵DE=PC=AC,
∵当DC=CP时,四边形DEPC为正方形,
此时DC=CP=AC,
∴△ACD为等腰直角三角形,
∴∠DAP=45°;
②∵DE=AC,DE∥AC,
∴四边形ACED为平行四边形,
∴AD∥CE,
∴∠ADC=∠DCE,
在Rt△ACD中,tan∠ADC=![]() =tan∠DCE=
=tan∠DCE=![]() ,
,
设AC=x,则DC=2x,
∴AD=![]() ,
,
在Rt△AOC中,AO=5,OC=CDOD=2x5,
∴x2+(2x5)2=52,解得x1=0(舍去),x2=4,
∴AD=![]() .
.
故答案为①45;②![]() .
.


科目:初中数学 来源: 题型:
【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
查看答案和解析>>
科目:初中数学 来源: 题型:
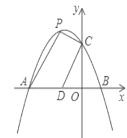
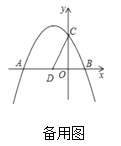
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
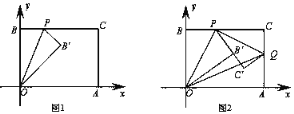
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
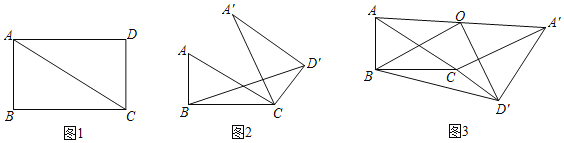
【题目】如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
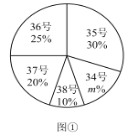
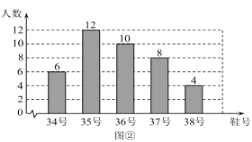
(Ⅰ)本次接受随机抽样调查的学生人数为________,图①中![]() 的值为________;
的值为________;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)根据样本数据,若学校计划购买150双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
,![]() ),E(0,
),E(0,![]() ),F(4,0)中,是⊙O的相邻点有__________;
),F(4,0)中,是⊙O的相邻点有__________;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程.
③点P在直线![]() 上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
上,若点P为⊙O的相邻点,求点P横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com