练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】对于题目“抛物线l1：（﹣1＜x≤2）与直线l2：y＝m（m为整数）只有一个交点，确定m的值”；甲的结果是m＝1或m＝2；乙的结果是m＝4，则（　　）

    A.只有甲的结果正确

    B.只有乙的结果正确

    C.甲、乙的结果合起来才正确

    D.甲、乙的结果合起来也不正确

    【答案】C

    【解析】

    画出抛物线l1：y＝﹣（x﹣1）2+4（﹣1＜x≤2）的图象，根据图象即可判断．

    解：由抛物线l1：y＝﹣（x﹣1）2+4（﹣1＜x≤2）可知抛物线开口向下，对称轴为直线x＝1，顶点为（1，4），

    如图所示：

    ∵m为整数，

    由图象可知，当m＝1或m＝2或m＝4时，抛物线l1：y＝﹣（x﹣1）2+4（﹣1＜x≤2）与直线l2：y＝m（m为整数）只有一个交点，

    ∴甲、乙的结果合在一起正确，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】打折前，买20件A商品和30件B商品要用2200元，买50件A商品和10件B商品要用2900元．若打折后，买40件A商品和40件B商品用了3240元，比不打折少花多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

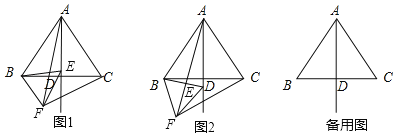
    【题目】已知△ABC是等边三角形，AD⊥BC于点D，点E是直线AD上的动点，将BE绕点B顺时针方向旋转60°得到BF，连接EF、CF、AF．

    （1）如图1，当点E在线段AD上时，猜想∠AFC和∠FAC的数量关系；（直接写出结果）

    （2）如图2，当点E在线段AD的延长线上时，（1）中的结论还成立吗？若成立，请证明你的结论，若不成立，请写出你的结论，并证明你的结论；

    （3）点E在直线AD上运动，当△ACF是等腰直角三角形时，请直接写出∠EBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中AB＝BC＝CD＝AD，∠BAD＝90°，对角线AC、BD相交于点O．

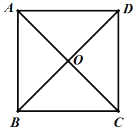
    （1）求证：四边形ABCD是正方形；

    （2）若P是对角线BD上任意一点，连接PA，PA绕点P逆时针旋转90°得到PE，连接AE、BE．

    ①根据题意画图，判断B、C、E三点是否共线，并说明理由；

    ②当BD＝8，△PBE的面积等于时，求PB的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

    （1）求水柱所在抛物线（第一象限部分）的函数表达式；

    （2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

    （3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

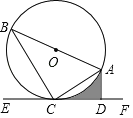
    【题目】如图，⊙O是Rt△ABC的外接圆，直径AB＝4，直线EF经过点C，AD⊥EF于点D，∠ACD＝∠B．

    （1）求证：EF是⊙O的切线；

    （2）若AD＝1，求BC的长；

    （3）在（2）的条件下，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（感知）如图①，点C是AB中点，CD⊥AB，P是CD上任意一点，由三角形全等的判定方法“SAS”易证△PAC≌△PBC，得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”

    （探究）如图②，在平面直角坐标系中，直线y=-x+1分别交x轴、y轴于点A和点B，点C是AB中点，CD⊥AB交OA于点D，连结BD，求BD的长

    （应用）如图③

    （1）将线段AB绕点A顺时针旋转90°得到线段AB′，请在图③网格中画出线段AB;

    （2）若存在一点P，使得PA=PB′，且∠APB′≠90°，当点P的横、纵坐标均为整数时，则AP长度的最小值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一对骰子，如果掷两骰子正面点数和为2、11、12，那么甲赢；如果两骰子正面的点数和为7，那么乙赢；如果两骰子正面的点数和为其他数，那么甲、乙都不赢.继续下去，直到有一个人赢为止.

    （1）你认为游戏是否公平？并解释原因；

    （2）如果你认为游戏公平，那么请你设计一个不公平的游戏；如果你认为游戏不公平，那么请你设计一个公平的游戏.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

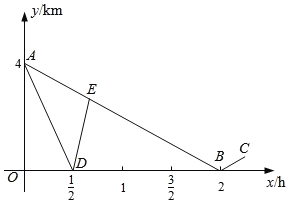
    【题目】某校学生步行到郊外春游，一班的学生组成前队，速度为4km/h，二班的学生组成后队，速度为6km/h．前队出发1h后，后队才出发，同时，后队派一名联络员骑自行车在两队之间不间断的来回进行联络，他骑车的速度为akm/h．若不计队伍的长度，如图，折线A﹣B﹣C，A﹣D﹣E分别表示后队、联络员在行进过程中，离前队的路程y（km）与后队行进时间x（h）之间的部分函数图象．

    （1）联络员骑车的速度a=　　　　 ；

    （2）求线段AD对应的函数表达式；

    （3）求联络员折返后第一次与后队相遇时的时间．

    查看答案和解析>>

    同步练习册答案