
【题目】一对骰子,如果掷两骰子正面点数和为2、11、12,那么甲赢;如果两骰子正面的点数和为7,那么乙赢;如果两骰子正面的点数和为其他数,那么甲、乙都不赢.继续下去,直到有一个人赢为止.
(1)你认为游戏是否公平?并解释原因;
(2)如果你认为游戏公平,那么请你设计一个不公平的游戏;如果你认为游戏不公平,那么请你设计一个公平的游戏.
科目:初中数学 来源: 题型:
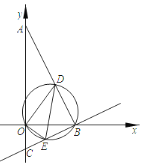
【题目】如图,在平面直角坐标系中,△ABC的顶点在坐标轴上,A,B,C三点的坐标分别为 (0,2),(1,0),(0,-0.5),D为线段AB上-个动点(不与点A,B重合),过B,D,0三点的圆与直线BC交于点E,当△OED面积取得最小值时,ED的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目“抛物线l1:![]() (﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
(﹣1<x≤2)与直线l2:y=m(m为整数)只有一个交点,确定m的值”;甲的结果是m=1或m=2;乙的结果是m=4,则( )
A.只有甲的结果正确
B.只有乙的结果正确
C.甲、乙的结果合起来才正确
D.甲、乙的结果合起来也不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
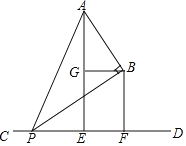
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
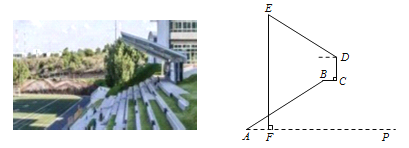
【题目】如图是某户外看台的截面图,长10m的看台AB与水平地面AP的夹角为35°,与AP平行的平台BC长为1.9m,点F是遮阳棚DE上端E正下方在地面上的一点,测得AF=2m,在挡风墙CD的点D处测得点E的仰角为26°,求遮阳棚DE的长. (参考数据:sin35°≈0.57,cos35°≈0.82, sin26°≈0.44,cos26°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
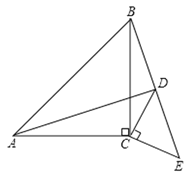
【题目】如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
(1)请探究AD与BD之间的位置关系并证明你的结论;
(2)若AC=BC=![]() ,DC=CE=
,DC=CE=![]() ,求线段AD的长;
,求线段AD的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回,搅匀,大量重复该实验,发现摸到绿球的频率稳定于0.2,求n的值;
(2)若![]() ,小明两次摸球(摸出一球后,不放回,再摸出一球),请用树状图画出小明摸球的所有结果,并求出两次摸出不同颜色球的概率.
,小明两次摸球(摸出一球后,不放回,再摸出一球),请用树状图画出小明摸球的所有结果,并求出两次摸出不同颜色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com