
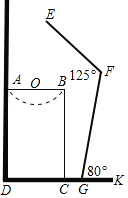
����Ŀ����ͼ��С��ϴ��ʱ�IJ���ʾ��ͼ��ϴ��̨������ABCD����ǽ�ڷţ���AD��80cm����AB��48cm��С������160cm���°���FG��100cm��ϴ��ʱ�°���������80������FGK��80����������ǰ���125������EFG��125����������ϴ��̨����GC��15cm����D��C��G��K��ͬһֱ���ϣ���
��1����ʱС��ͷ��E�������DK�����٣�
��2����С��ͷ��Eǡ����ϴ����AB���е�O�����Ϸ�����Ӧ��ǰ������ƶ��������ף���sin80���0.98��cos80���0.18��![]() ��1.41�������ȷ��0.1��
��1.41�������ȷ��0.1��
���𰸡���1��140.3cm����2��14.7cm
��������
��1������F��FN��DK��N������E��EM��FN��M�����MF��FN��ֵ���ɽ�����⣻
��2�����OH��PH��ֵ�����жϣ�
�⣺��1������F��FN��DK��N������E��EM��FN��M��
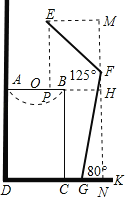
��EF+FG��160��FG��100��
��EF��60��
�ߡ�FGK��80����
��FN��100sin80���98
�ߡ�EFG��125����
���EFM��180����125����10����45����
��FM��60cos45����30![]() ��42��3��
��42��3��
��MN��FN+FM��140��3��
���ʱС��ͷ��E�������DK���ԼΪ140.3cm��
��2������E��EP��AB�ڵ�P���ӳ�OB��MN��H��
��AB��48��OΪAB�е㣬
��AO��BO��24��
��EM��60sin45���42��3��
��PH��42��3��
��GN��100cos80���18��CG��15��
��OH��24+15+18��57��OP��OH��PH��57��42��3��14��7��
����Ӧ��ǰ14.7cm��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��涨��һ��������ԭ����ʱ����ת45������������ת��ĵ����ԭ��ĶԳƵ㣬���Ϊһ�α任����֪��A������Ϊ����1��0�������A��������2018�������ı任�õ��ĵ�A2018��������___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
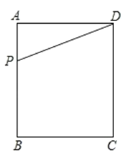
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ����
����![]() �DZ�
�DZ�![]() �ϵ�һ���㣬����
�ϵ�һ���㣬����![]() ��
��
��1������![]() ��
��![]() �۵�����
�۵�����![]() ���ھ��εĶԽ����ϵ�
���ھ��εĶԽ����ϵ�![]() ��������
��������![]() �ij���
�ij���
��2����![]() �˶���ijһʱ�̣�����
�˶���ijһʱ�̣�����![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �۵�����
�۵�����![]() ���
���![]() �ֱ����ڵ�
�ֱ����ڵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����ǡ����ͬһֱ���ϣ���
����ǡ����ͬһֱ���ϣ���![]() �����ʱ
�����ʱ![]() �ij���
�ij���
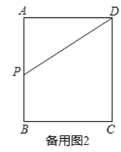
��3������![]() �˶�����
�˶�����![]() ���е㴦ʱ������
���е㴦ʱ������![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �۵�����
�۵�����![]() ���
���![]() �غ��ڵ�
�غ��ڵ�![]() ��������
��������![]() �������
�������![]() �ij���
�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
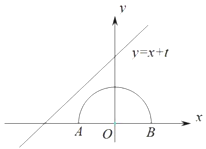
����Ŀ����ͼ����Բ��Բ��������ԭ���غϣ���Բ�İ뾶1��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��ֱ��
��ֱ��![]() ���Բֻ��һ�����㣬��t��ȡֵ��Χ��________��
���Բֻ��һ�����㣬��t��ȡֵ��Χ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����ɸ��뾶Ϊ3����λ���ȣ�Բ�Ľ�Ϊ60�����������һ�����������ߣ���P��ԭ��O����������������������������˶�������ֱ���ϵ��ٶ�Ϊÿ��3����λ���ȣ����ڻ����ϵ��ٶ�Ϊÿ��������λ���ȣ���2020��ʱ����P�������ǣ�������
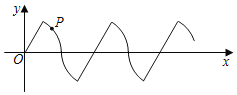
A.��2020��0��B.��3030��0��C.�� 3030��![]() ��D.��3030����
��D.��3030����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ���㣨0��1�����Գ���Ϊֱ��x=��1�����н��ۣ���a+b+c��0����a��b+c��1����abc��0����4a��2b+c��0����c��a��1�����У���ȷ���۵ĸ���Ϊ��������
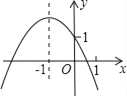
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ȳ���Ŀ���ʶ��ߡ�������ѧ�����Ķ���Ȥ��ijУΪ����ѧ�����Ķ�����������һ��ѧ��ϲ����ͼ�飬ѧУ��֯ѧ�����Ա�����ȡ����ѧ�������ʾ����飬������ѧ����ӡ���ʷ�ࡢ����ࡢС˵�ࡢ�����ࡱ��ѡ���Լ�ϲ����һ�࣬���ݵ�����������ͳ��ͼ��δ��ɣ��������ͼ����Ϣ������������⣺
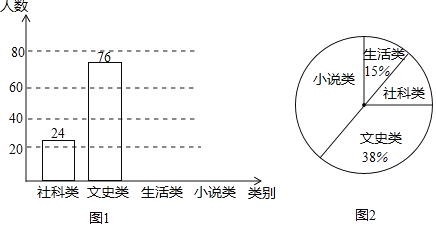
��1���˴ι��������� ����ѧ����
��2��������ͳ��ͼ1����������
��3��ͼ2�С�С˵�ࡱ�������ε�Բ�Ľ�Ϊ�� ���ȣ�
��4������У����ѧ��2000�ˣ����Ƹ�Уϲ��������ࡱ�鼮��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ����������֧�����������������������������������ǵ���������˺ܶ������������ѧС����У�ڶ��������Ͽɵ��Ĵ��������������е��飬���������m�ˣ�ÿ��ѧ����ѡһ����ֻ�ܴ���������ѡ��һ�֣��������������Ƴ����²�������ͳ��ͼ��

��1������ͼ����Ϣ���m=�� ����n=�� ����
��2������������ǽ�������ͳ��ͼ��ȫ��
��3�����ݳ�������Ľ���������ȫУ2000��ѧ���У���Լ�ж��������Ͽ���������һ�������
��4����֪A��B��λͬѧ�����Ͽ���������Cͬѧ���Ͽ���֧������Dͬѧ���Ͽ�����������������ͬѧ�г�ȡ����ͬѧ������ͨ����״ͼ������������λͬѧ���Ͽɵ��������ﲻһ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
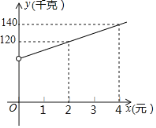
����Ŀ��������ij��ó��˾��ÿǧ��40Ԫ�ļ۸�һ�ָɹ����ƻ���ÿǧ��60Ԫ�ļ۸����ۣ�Ϊ���ù˿͵õ������ʵ�ݣ��־����������ۣ���֪���ָɹ�������y(ǧ��)��ÿǧ�˽���x(Ԫ)(0��x��20)֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)��ó��˾Ҫ�����2090Ԫ�������ָɹ�ÿǧ��Ӧ���۶���Ԫ��
(3)�øɹ�ÿǧ�˽��۶���Ԫʱ����ó��˾���������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com