
【题目】如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 ( )

A.5B.6C.8D.10
科目:初中数学 来源: 题型:
【题目】如图,AB//CD.

(1)如图①,若∠ABE=40o,∠BEC=140o,∠ECD=_________o
(2)如图①,试探究∠ABE,∠BEC,∠ECD的关系,并说明理由;
(3)如图②,若CF平分∠ECD,且满足CF∥BE,试探究∠ECD,∠ABE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)己知2a-1的平方根是土3,3a+b-1的平方根是土4,c是![]() 的整数部分,求a+2b+c的算术平方根.
的整数部分,求a+2b+c的算术平方根.
(2)已知在△ABC中,AB=10,BC=21,AC=17,则△ABC面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近雾霾天气频繁,使得空气净化器得以畅销.某商场代理销售某种空气净化器,其进价是500元/台,经过市场销售后发现,当售价是1000元/台时,每月可售出50台,且售价每降低20元,每月就可多售出5台.若供货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出自变量x的取值范围.
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿![]() 轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
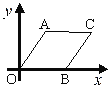
A. (-3,-1) B. (3,1) C. (3,1)(-3,-1) D. (-3,1)(3,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府为响应党中央建设社会主义新农村和节约型社会的号召,决定资助部分农村地区修建一批沼气池,使农民用到经济.环保的沼气能源.红星村共有360户村民,村里得到34万元的政府资助款,准备再从各户筹集一部分资金修建A型.B型沼气池共20个,两种型号沼气池每个修建费用,可供使用的户数.修建用地情况见下表:
沼气池 | 维修费用 (万元/个) | 可供使用户数 (户/个) | 占地面积 (平方米/个) |
A型 | 3 | 20 | 24 |
B型 | 2 | 15 | 19 |
政府土地部分只批给该沼气池修建用地450平方米,
(1)试问有哪几种满足以上要求的修建方案?
(2)平均每村民筹集500元钱,能否满足所需费用最少的修建方案?
(3)在(2)问下,若每个A型沼气池可不需维修使用8年,每年可节省能源费1200元,每个B型沼气池可不需维修使用7年,每年可节省能源消费700元.两种沼气池使用寿命到期后,每个需投资1000元维修,可继续使用相同时间,村民最快多少年后可收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
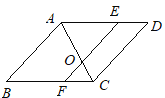
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com