
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿![]() 轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
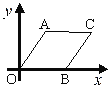
A. (-3,-1) B. (3,1) C. (3,1)(-3,-1) D. (-3,1)(3,-1)
【答案】D
【解析】
根据菱形的对称性求出点B的坐标,再求出AB的中点的坐标,进而求出点C的坐标,根据向左平移横坐标减,向下平移纵坐标减求出平移后的C点对应的坐标,结合翻折变换知识求出沿x轴翻折后C点对应的坐标,再根据旋转的性质确定点P的坐标.
∵菱形AOBC的点A坐标为(3,4),
∴点B的坐标为(5,0),
∴AB的中点的坐标为(4,2),
∴点C坐标为(8,4),
∵向左平移9个单位长度,再向下平移1个单位长度,
∴8-9=-1,4-1=3,
∴平移后点C对应的坐标为(-1,3),
沿x轴翻折后C点对应的坐标为(-1,-3),
∵在坐标平面内绕点O旋转90°,
∴若是顺时针旋转,则对应点在第二象限,坐标为(-3,1),
若是逆时针旋转,则对应点在第四象限,坐标为(3,-1),
综上所述,点P的坐标为(-3,1)或(3,-1),
故选:D


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该电子产品的生产成本为每件40元,公司每月要支付其他费用15万元.该产品每月的销售量y(万件)与销售单价x(元)满足如图所示的一次函数关系:
(1)求每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)当销售单价定为多少元时,该公司每月销售利润最大.
(3)若相关部门要求该电子产品的销售单价不得低于其生产成本,且销售每件产品的利润率不能超过25%,则该公司最早用几个月可以还清无息贷款?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 ( )

A.5B.6C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都是全国最佳旅游城市,某校摄影社团在“最美锦城”主题宣传周里,设计了五条精品旅游路线:![]() 草堂寻诗,
草堂寻诗,![]() 观鸟白鹭湾,
观鸟白鹭湾,![]() 三圣赏花,
三圣赏花,![]() 探秘金沙,
探秘金沙,![]() 拜相武侯祠.随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图,请解决下列问题.
拜相武侯祠.随机抽取部分学生举行“最爱旅游路线”投票活动,参与者每人选出一条最爱的旅游路线,社团对投票进行了统计,并绘制出如下不完整的条形统计图和扇形统计图,请解决下列问题.

(1)参与本次投票的总人数是_________人,并补全条形统计图;
(2)扇形统计图中,线路![]() 部分的圆心角是_______度;
部分的圆心角是_______度;
(3)若该校共有1200名学生,请估计选择路线“![]() 拜相武侯祠”的学生有多少?
拜相武侯祠”的学生有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=AD,∠BAD=90°,P是CD边上一点,连结PA,分别过点B,D作BE⊥PA,DF⊥PA,垂足分别为点E,F,如图①

(1)求证:BE=DF+EF;
(2)若点P在DC的延长线上,如图②,上述结论还成立吗?如果成立请写出证明过程;如果不成立,请写出正确结论并加以证明.
(3)若点P在CD的延长线上,如图③,那么这三条线段的数量关系是 .(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com