
【题目】尺规作图:过直线外一点作已知直线的平行线.
已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

作法如下:
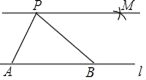
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.

请回答:PM平行于l的依据是_____.
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
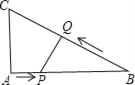
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=
与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=![]() .
.
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;
(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
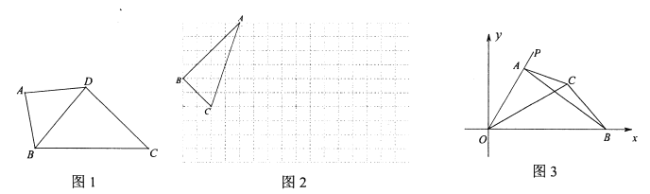
(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(2)如图2,已知格点![]() ,请你在正方形网格中画出所有的格点四边形
,请你在正方形网格中画出所有的格点四边形![]() ,使四边形
,使四边形![]() 是以
是以![]() 为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
(3)如图3,四边形![]() 中,点
中,点![]() 在射线
在射线![]() :
:![]() 上,点
上,点![]() 在
在![]() 轴正半轴上,对角线
轴正半轴上,对角线![]() 平分
平分![]() ,连接
,连接![]() .若
.若![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P.
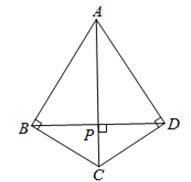
(1)请作出Rt△ABC的外接圆⊙O;(保留作图痕迹,不写作法)
(2)点D在⊙O上吗?说明理由;
(3)试说明:AC平分∠BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;②折叠后∠ABE和∠CBD一定相等;③折叠后得到的图形是轴对称图形;④△EBA和△EDC一定是全等三角形.其中正确的是( )

A. ①②③B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,抛物线y=ax2+bx+3与x轴交于点B、C,与y轴交于点A,且AO=CO,BC=4.
(1)求抛物线解析式;
(2)如图2,点P是抛物线第一象限上一点,连接PB交y轴于点Q,设点P的横坐标为t,线段OQ长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,过点Q作直线l⊥y轴,在l上取一点M(点M在第二象限),连接AM,使AM=PQ,连接CP并延长CP交y轴于点K,过点P作PN⊥l于点N,连接KN、CN、CM.若∠MCN+∠NKQ=45°时,求t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
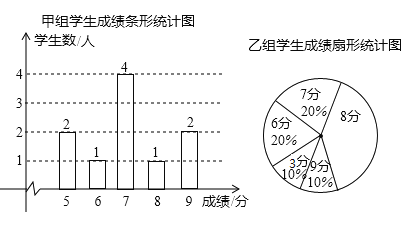
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com