
分析 (1)(2)由题意可知:从1开始连续自然数的立方和,等于最后一个自然数的平方乘这个自然数加1的平方的$\frac{1}{4}$,由此规律计算得出答案即可;
(3)由(2)的结果减去(1)的结果即可.
解答 解:(1)13+23+33+43+…+103=$\frac{1}{4}$×102×112;
(2)13+23+33+…+993+1003
=$\frac{1}{4}$×1002×1012
=25502500;
(3)$\frac{1}{4}$×1002×1012-$\frac{1}{4}$×102×112
=25502500-3025
=25499475.
点评 此题考查数字的变化规律,抓住数字特点,找出数字之间的运算规律,利用规律解决问题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
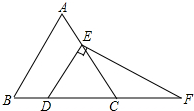 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
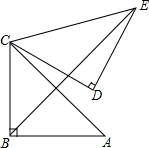 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 75.01 | B. | 75.49 | C. | 74.99 | D. | 74.49 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com