
【题目】在平面直角坐标系xOy中,二次函数C1:![]() (m>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(m>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A和点C的坐标;
(2)当AB=4时,
①求二次函数C1的表达式;
②在抛物线的对称轴上是否存在点D,使△DAC的周长最小,若存在,求出点D的坐标,若不存在,请说明理由;
(3)将(2)中抛物线C1向上平移n个单位,得到抛物线C2,若当0≤x≤![]() 时,抛物线C2与x轴只有一个公共点,结合函数图象,求出n的取值范围.
时,抛物线C2与x轴只有一个公共点,结合函数图象,求出n的取值范围.
【答案】(1)A(-1,0);C(0,-3);(2)①![]() ;② D(1,-2);(3)
;② D(1,-2);(3)![]() ≤n<3或n=4.
≤n<3或n=4.
【解析】
(1)解方程![]() 即可得到点A、B的坐标;在函数
即可得到点A、B的坐标;在函数![]() 中,由x=0可得y=-3,由此可得点C的坐标;
中,由x=0可得y=-3,由此可得点C的坐标;
(2)①由(1)中所得点A、B的坐标结合AB=4可得m的值,由此即可得到函数的解析式;②由题意可知,AC是定值,而A、B两点关于抛物线的对称轴对称,由此可知当点D为直线BC与抛物线的对称轴的交点时,△ACD的周长最小,故由已知条件求得直线BC的解析式,再求出BC与对称轴的交点的坐标即可;
(3)①由题意设平移后的抛物线C2的解析式为:![]() ,当平移后的抛物线过点(
,当平移后的抛物线过点(![]() ,0)和(0,0)时,由抛物线的对称轴为直线x=1可得抛物线与x轴的另一个交点为(-0.5,0)和(1,0),由点(-0.5,0)不在
,0)和(0,0)时,由抛物线的对称轴为直线x=1可得抛物线与x轴的另一个交点为(-0.5,0)和(1,0),由点(-0.5,0)不在![]() 的范围内,点(1,0)在
的范围内,点(1,0)在![]() 可求得n的一个符合题意的取值范围; ②当平移后的抛物线
可求得n的一个符合题意的取值范围; ②当平移后的抛物线![]() 的顶点在x轴上时,新抛物线与x轴也只有一个交点(1,0)在
的顶点在x轴上时,新抛物线与x轴也只有一个交点(1,0)在![]() 的范围内,由此也可得到一个符合条件的n的值;综合①②即可得到n的取值范围.
的范围内,由此也可得到一个符合条件的n的值;综合①②即可得到n的取值范围.
(1)在二次函数![]() 中,当y=0时,可得方程:
中,当y=0时,可得方程:
![]() ,
,
解得:![]() ,
,
∵抛物线![]() 与x轴的交点A在点B的左侧,且m>0,
与x轴的交点A在点B的左侧,且m>0,
∴点A的坐标为(-1,0),点B的坐标为(![]() ,0),
,0),
∵在![]() 中,当x=0时,y=-3,
中,当x=0时,y=-3,
∴点C的坐标为(0,-3);
(2)①∵点A的坐标为(-1,0),点B的坐标为(![]() ,0),且m>0,
,0),且m>0,
∴AB=![]() +1,
+1,
又∵AB=4,
∴![]() +1=4,解得m=1,
+1=4,解得m=1,
∴抛物线的解析式为:![]() ;
;
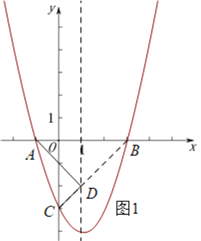
②如图1,由m=1,可得点B的坐标为(3,0),
∵AC的长为定值,A、B两点关于抛物线的对称轴x=1对称,
∴当点D为直线BC与对称轴x=1的交点时,AD+CD最小,此时△ACD的周长最小,
∵点B的坐标为(3,0),点C的坐标为(0,-3),
∴直线BC的表达式为 y=x-3.
把x=1代入y=x-3得y=-2,
∴D(1,-2);
(3)设抛物线C2的表达式为![]()
①当抛物线C2经过点(![]() ,0)时,解得:n =
,0)时,解得:n =![]() ,此时抛物线与x轴的另一个交点为(-0.5,0),该点不在
,此时抛物线与x轴的另一个交点为(-0.5,0),该点不在![]() 范围内;
范围内;
当抛物线C2经过点(0,0)时,解得得n=3,此时抛物线与x轴的另一个交点为(1,0),该点在![]() 的范围内,
的范围内,
∴综上可得:![]() ≤n<3 ;
≤n<3 ;
②当抛物线![]() 的顶点在x轴上时,抛物线C2与x轴只有一个公共点,此时有x=1,y=0,解得n=4;
的顶点在x轴上时,抛物线C2与x轴只有一个公共点,此时有x=1,y=0,解得n=4;
综合①②可得,n的取值范围是![]() ≤n<3或n=4.
≤n<3或n=4.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
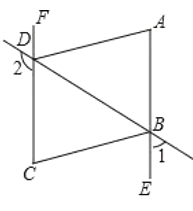
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
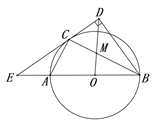
【题目】如图,Rt△ABC中,∠C=90°,⊙O是Rt△ABC的外接圆,过点C作⊙O的切线交BA的延长线于点E,BD⊥CE于点D,连接DO交BC于点M.
(1)求证:BC平分∠DBA;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动(
向左运动(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上),运动的时间为
上),运动的时间为![]() .
.

(1)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(2)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(3)若![]() 、
、![]() 运动到任一时刻时,总有
运动到任一时刻时,总有![]() ,请求出
,请求出![]() 的长;
的长;
(4)在(3)的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
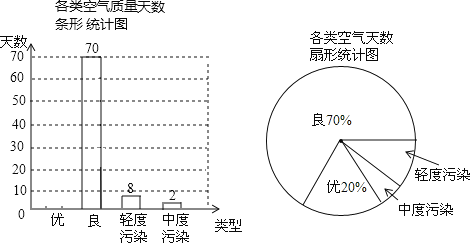
【题目】空气质量倍受人们关注,我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了1月至4月份若干天的空气质量情况,并绘制了如下不完整的统计图,请根据图中信息,解决下列问题:
(1)统计图共统计了________天的空气质量情况;
(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形的圆心角度数;
(3)小明所在环保兴趣小组共4名同学(2名男同学,2名女同学).随机选取两名同学去该空气质量监涮站点参观,请用列表或画树状图的方法求出恰好选到一名男同学和一名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
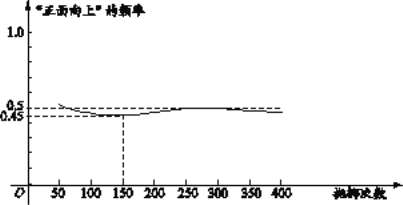
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com