
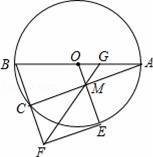
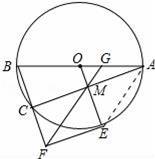
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
(1)求∠AMO;
(2)延长OM交⊙O于点E,过E作⊙O的切线,交BC延长线于点F,连接FM,并延长FM交AB于点G.
①试判断四边形CFEM的形状,并说明理由;
②若AG=2,CM=3,求四边形CFEM的面积.

【考点】圆的综合题.
【分析】(1)根据两直线平行同位角相等即可解决问题.
(2)①先证明四边形CFEM是平行四边形,再证明有一个角为90°即可.
②连接AE,只要证明OG=OM,即可得到EM=AG,即可解决问题.
【解答】解:(1)∵AB为直径,
∴∠BCA=90°,
∵OM∥BC,
∴∠AMO=∠BCA=90°.
(2)①四边形CMEF为矩形,理由如下:
∵EF与⊙O相切于点E,
∴∠OEF=90°,
∵∠OMA=∠OMC=∠OEF=90°,
∴EF∥MC,
∵OM∥BC,
∴EM∥FC,
∴四边形CMEF为平行四边形,
∵∠OEF=90°,
∴四边形CMEF为矩形.
②解:连接AE,
∵O为AB的中点,OM∥BC
∴M为AC的中点,即有CM=AM,
∵四边形CMEF是矩形,
∴AM=CM=EF,
又∵AC∥EF,
∴AMFE为平行四边形,
∴FM∥AE,即GM∥AE,
∴∠OMG=∠OEA,∠OGM=∠OAE
∵OE=OA
∴∠OEA=∠OAE,
∴∠OMG=∠OGM,
∴OM=OG
∵OE=OM+ME=OA=OG+GA,
∴ME=GA=2,
∴矩形CMEF的面积为:CM×ME=3×2=6.

【点评】本题考查圆的有关知识、等腰三角形的判定好性质、矩形的判定和性质、平行四边形的判定和性质等知识,解题的关键是平行四边形AEFM的发现,需要灵活应用这些知识,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
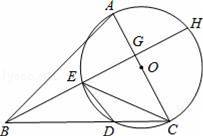
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧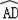
 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
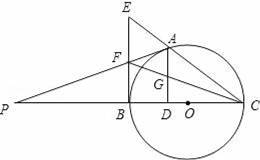
如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.则以下四个结论:①BF=EF;②PA⊥OA;③tan∠P=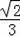
 ;④OC=3
;④OC=3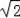
 ,上述结论中正确的有 (填番号).
,上述结论中正确的有 (填番号).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )


A.ab>0 B.a+b>0 C.(a﹣1)(b﹣1)>0 D.(a+1)(b﹣1)>0
查看答案和解析>>
科目:初中数学 来源: 题型:
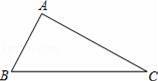
如图,在△ABC中,AB=4cm,AC=6cm.
(1)作图:作BC边的垂直平分线分别交与AC,BC于点D,E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结BD,求△ABD的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com