
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
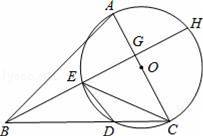

【考点】圆周角定理;勾股定理;相似三角形的判定与性质.
【专题】几何综合题;压轴题.
【分析】(1)连接AD,由圆周角定理即可得出∠DAC=∠DEC,∠ADC=90°,再根据直角三角形的性质即可得出结论;
(2)由∠BDA=180°﹣∠ADC=90°,∠ABC=45°可求出∠BAD=45°,利用勾股定理即可得出DC的长,进而求出BC的长,由已知的一对角线段和公共角,根据两对对应角相等的两三角形相似可得三角形BCE与三角形EDC相似,由相似得比例即可求出CE的长.
【解答】(1)证明:连接AD,
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,
∴∠BGC=180°﹣(∠EBC+∠DCA)=180°﹣90°=90°,
∴AC⊥BH;
(2)解:∵∠BDA=180°﹣∠ADC=90°,∠ABC=45°,
∴∠BAD=45°,
∴BD=AD,
∵BD=8,∴AD=8,
在直角三角形ADC中,AD=8,AC=10,
根据勾股定理得:DC=6,则BC=BD+DC=14,
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD,
∴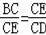
 ,即CE2=BC•CD=14×6=84,
,即CE2=BC•CD=14×6=84,
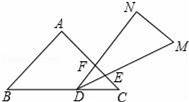
∴CE=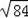
 =2
=2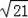
 .
.

【点评】本题考查的是圆周角定理,相似三角形的判定与性质及勾股定理,根据题意作出辅助线是解答此题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )


A.300 B.315 C.279 D.342
查看答案和解析>>
科目:初中数学 来源: 题型:
下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是( )
A.①② B.①③ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
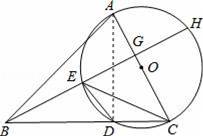
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E、F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )
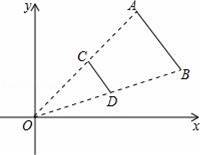

A.(3,3) B.(4,3) C.(3,1) D.(4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
(1)求∠AMO;
(2)延长OM交⊙O于点E,过E作⊙O的切线,交BC延长线于点F,连接FM,并延长FM交AB于点G.
①试判断四边形CFEM的形状,并说明理由;
②若AG=2,CM=3,求四边形CFEM的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com