练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数与反比例函数的图象交于A（1，8）和B（4，2）两点，点P是线段AB上一动点（不与点A和B重合），过P点分别作x轴，y轴的垂线PC，PD交反比例函数图象于点E，F，则四边形OEPF面积的最大值是（　　）

    A.3B.4C.D.6

    【答案】C

    【解析】

    利用A和B两个点求出解析式，将面积转化为二次函数的形式，利用二次函数的性质求最大值．

    解：设一次函数解析式为y＝kx+b，反比例函数解析式为y＝，

    ∵A（1，8）和B（4，2）是两个函数图象的交点，

    ∴y＝，

    ∴，

    ∴，

    ∴y＝﹣2x+10，

    ∵S△ODF＝S△ECO＝4，

    设点P的坐标（x，﹣2x+10），

    ∴四边形OEPF面积＝xy﹣8＝x（﹣2x+10）﹣8＝﹣2x2+10x﹣8＝﹣2（x﹣）2+，

    ∴当x＝时，面积最大为；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，把绕点旋转到，当点D刚好落在上时，连结，设，相交于点，则图中相似三角形（不含全等）的对数有（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校组织学生书法比赛，对参赛作品按A、B、C、D四个等级进行了评定．现随机抽取部分学生书法作品的评定结果进行分析，并绘制扇形统计图和条形统计图如下：

    根据上述信息完成下列问题：

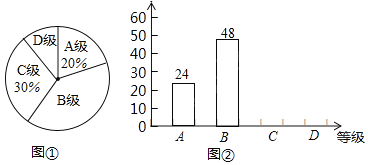
    （1）在这次抽样调查中，共抽查了多少名学生？

    （2）请在图②中把条形统计图补充完整；

    （3）求出扇形统计图中“D级”部分所对应的扇形圆心角的大小；

    （4）已知该校这次活动共收到参赛作品750份，请你估计参赛作品达到B级以上（即A级和B级）有多少份？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

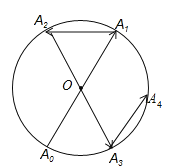
    【题目】如图所示，一动点从半径为2的上的点出发，沿着射线方向运动到上的点处，再向左沿着与射线夹角为的方向运动到上的点处；接着又从点出发，沿着射线方向运动到上的点处，再向左沿着与射线夹角为的方向运动到上的点处；间的距离是________；…按此规律运动到点处，则点与点间的距离是________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点是反比例函数的图象上任意一点，轴交反比例函数的图象于点，以为边作，其中、在轴上，则为（ ）

    A.2B.3C.4D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．

    （1）求该旅行团中成人与少年分别是多少人?

    （2）因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．

    ①若由成人8人和少年5人带队，则所需门票的总费用是多少元?

    ②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的是（ ）

    A.了解全市中学生对社会主义核心价值观的知晓度的情况，适合用抽样调查

    B.若甲组数据方差S2甲＝0.39，乙组数据方差S2乙＝0.27，则乙组数据比甲组数据稳定

    C.某种彩票中奖的概率是，买100张该种彩票一定会中奖

    D.旅客上飞机前的安检应该进行全面调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线经过点，现将抛物线沿轴翻折，并向左平移1个单位长度后得到物线．

    （1）求抛物线的解析式．

    （2）若抛物线与轴交于，两点（点在点右侧），点在抛物线对称轴上一点，为坐标原点，则抛物线上是否存在点，使以，，，为顶点的四边形是干行四边形？若存在，求出点的坐标：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

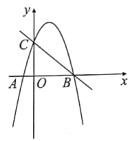
    【题目】如图所示，二次函数的图象与轴交于点、，与轴交于点，直线经过点、．

    （1）求抛物线的表达式；

    （2）过点的直线交抛物线于点，交直线于点，连接，当直线平分的面积时，求点的坐标；

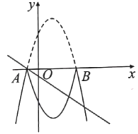
    （3）如图所示，把抛物线位于轴上方的图象沿轴翻折，当直线与翻折后的整个图象只有三个交点时，求的取值范围．

    查看答案和解析>>

    同步练习册答案