
【题目】已知抛物线![]() 经过点
经过点![]() ,现将抛物线
,现将抛物线![]() 沿
沿![]() 轴翻折,并向左平移1个单位长度后得到物线
轴翻折,并向左平移1个单位长度后得到物线![]() .
.
(1)求抛物线![]() 的解析式.
的解析式.
(2)若抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),点
右侧),点![]() 在抛物线
在抛物线![]() 对称轴上一点,
对称轴上一点,![]() 为坐标原点,则抛物线
为坐标原点,则抛物线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是干行四边形?若存在,求出点
为顶点的四边形是干行四边形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)将点![]() 坐标代入解析式可求抛物线
坐标代入解析式可求抛物线![]() 的解析式,由轴对称和平移的性质可求解;
的解析式,由轴对称和平移的性质可求解;
(2)分别以![]() 为边或
为边或![]() 为对角线两种情况讨论,由平行四边形的性质和中点坐标公式可求解.
为对角线两种情况讨论,由平行四边形的性质和中点坐标公式可求解.
解:(1)∵拋物线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() ,
,
∵抛物线![]() 沿
沿![]() 轴翻折,并向左平移1个单位长度后得到抛物线
轴翻折,并向左平移1个单位长度后得到抛物线![]() .
.
∴抛物线![]() 的解析式为:
的解析式为:![]() ;
;
(2)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),
右侧),
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() ,点
,点![]() ,
,
∵点![]() 在拋物线
在拋物线![]() 对称轴上一点,
对称轴上一点,
∴点![]() 的横坐标为
的横坐标为![]() ,
,
若![]() 为边,则
为边,则![]() ,
,![]()
∴点![]() 的横坐标为:
的横坐标为:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() ,
,
当![]() ,
,![]() ,
,
∴点![]() ;
;
若![]() 为对角线,
为对角线,
∴![]() 的中点坐标为
的中点坐标为![]()
∴点![]() 的横坐标为6,
的横坐标为6,
∴![]() ,
,
∴点![]() ,
,
综上所述:当点![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() 时,以
时,以![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与反比例函数的图象交于A(1,8)和B(4,2)两点,点P是线段AB上一动点(不与点A和B重合),过P点分别作x轴,y轴的垂线PC,PD交反比例函数图象于点E,F,则四边形OEPF面积的最大值是( )

A.3B.4C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC为等腰直角三角形∠ACB=90°,过点C作直线CM,D为直线CM上一点,如果CE=CD且EC⊥CD.
(1)求证:△ADC≌△BEC;
(2)如果EC⊥BE,证明:AD∥EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 、
、![]() 是紧靠某湖泊的两条相互垂直的公路,曲线段
是紧靠某湖泊的两条相互垂直的公路,曲线段![]() 是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路
是该湖泊环湖观光大道的一部分.现准备修建一条直线型公路![]() ,用以连接两条公路和环湖观光大道,且直线
,用以连接两条公路和环湖观光大道,且直线![]() 与曲线段
与曲线段![]() 有且仅有一个公共点
有且仅有一个公共点![]() .已知点
.已知点![]() 到
到![]() 、
、![]() 的距离分别为
的距离分别为![]() 和
和![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]() .若分别以
.若分别以![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,则曲线段
,则曲线段![]() 对应的函数解析式为
对应的函数解析式为![]() .
.
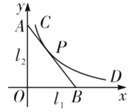
(1)求![]() 的值,并指出函数
的值,并指出函数![]() 的自变量的取值范围;
的自变量的取值范围;
(2)求直线![]() 的解析式,并求出公路
的解析式,并求出公路![]() 的长度(结果保留根号).
的长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
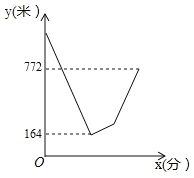
【题目】某个周末小月和小华在南滨路跑步锻炼身体,两人同时从A点出发,沿直线跑到B点后马上掉头原路返回A点算一个来回,回到A点后又马上调头去往B点,以此类推,每人要完成2个来回。一直两人全程均保持匀速,掉头时间忽略不计。如图所示是小华从出发到他率先完成第一个来回为止,两人到B点的距离之和y(米)与小华跑步时间x(分钟)之间的函数图像,则当小华跑完2个来回时,小月离B点的距离为___米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在学习完一次函数与反比例函数的图象与性质后,对函数图象与性质研究饶有兴趣,便想着将一次函数与反比例函数的解析式进行组合研究.他选取特殊的一次函数![]()
![]() 与反比例函数
与反比例函数![]()
![]() ,相加后,得到一个新的函数
,相加后,得到一个新的函数![]()
![]() .已知,这个新函数满足:当
.已知,这个新函数满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求出小林研究的这个组合函数的解析式;
(2)小林依照列表、描点、连线的方法在给定的平面直角坐标系内画出了该函数图象的一部分,请你在图中补全小林未画完的部分,并根据图象,写出该函数图象的一条性质;
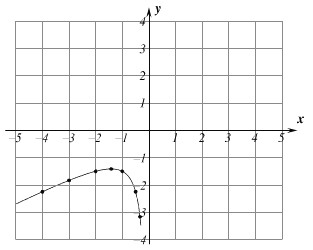
(3)请根据你所画的函数图象,利用所学函数知识,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
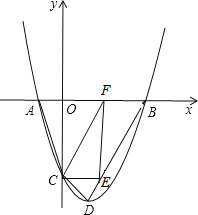
【题目】如图抛物线y=x2+bx+c(c<0)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C,顶点为D,且OB=OC=3,点E为线段BD上的一个动点,EF⊥x轴于F.
(1)求抛物线的解析式;
(2)是否存在点E,使△ECF为直角三角形?若存在,求点E的坐标;不存在,请说明理由;
(3)连接AC、BC,若点P是抛物线上的一个动点,当P运动到什么位置时,∠PCB=∠ACO,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com