
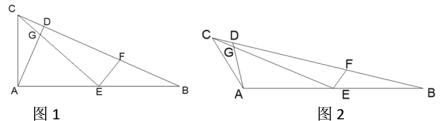
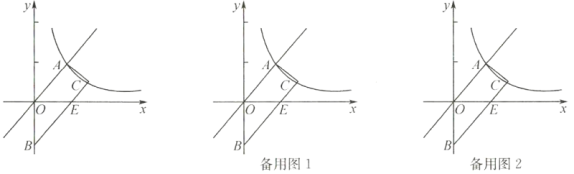
【题目】如图,在△ABC中,AB=2AC, 点D在BC上,且∠CAD=∠B,点E是AB的中点,联结CE与AD交于点G,点F在BC上,且∠CEF=∠BAC.
(1)若∠BAC=90°,如图1,求证: EG+ EF=![]() AC;
AC;
(2)若∠BAC=120°,如图2,请猜想线段EG,EF和AC之间的数量关系并证明.
【答案】(1)见解析;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)首先根据∠BAC=90°, ∠CEF=∠BAC得出∠CEF=90°,进而得出∠AEC+∠BEF=90°,又由AB=2AC, 点E是AB的中点,得出AC=AE=BE,进而得出∠ACE=∠AEC=45°,CE=![]() ,∠BEF=45°,再由∠CAD=∠B,得出∠B+∠ACB=∠CAD+∠ACB=90°,进而得出∠ADC=90°,即可判定△ACG≌△BEF,得出CG=EF,即可得出EG+ EF=
,∠BEF=45°,再由∠CAD=∠B,得出∠B+∠ACB=∠CAD+∠ACB=90°,进而得出∠ADC=90°,即可判定△ACG≌△BEF,得出CG=EF,即可得出EG+ EF=![]() AC;
AC;
(2)首先过点A作AH⊥EC,由∠BAC=120°, ∠CEF=∠BAC,得出∠CEF=120°,进而得出∠AEC+∠BEF=60°,又由AB=2AC, 点E是AB的中点,得出AC=AE=BE,进而得出∠ACE=∠AEC=30°,∠BEF=30°,可判定△ACG≌△BEF,得出CG=EF,又由AH⊥EC,得出EH=CH=![]() EC=
EC=![]() ,即可得出
,即可得出![]() .
.
(1)∵∠BAC=90°, ∠CEF=∠BAC
∴∠CEF=90°
∴∠AEC+∠BEF=90°
又∵AB=2AC, 点E是AB的中点,
∴AC=AE=BE
∴∠ACE=∠AEC=45°,CE=![]()
∴∠BEF=45°
又∵∠CAD=∠B,
∴∠B+∠ACB=∠CAD+∠ACB=90°
∴∠ADC=90°
在△ACG和△BEF中,
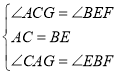
∴△ACG≌△BEF(ASA)
∴CG=EF
∴EG+ EF=![]() AC
AC
(2)![]()
过点A作AH⊥EC,交CE于点H,如图所示
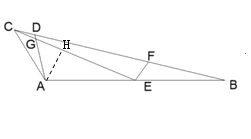
∵∠BAC=120°, ∠CEF=∠BAC
∴∠CEF=120°
∴∠AEC+∠BEF=60°
又∵AB=2AC, 点E是AB的中点,
∴AC=AE=BE
∴∠ACE=∠AEC=30°,
∴∠BEF=30°
在△ACG和△BEF中,
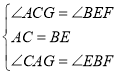
∴△ACG≌△BEF(ASA)
∴CG=EF
又∵AH⊥EC,
∴EH=CH=![]() EC=
EC=![]()
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】武胜县白坪—飞龙乡村旅游度假村橙海阳光景点组织![]() 辆汽车装运完
辆汽车装运完![]() 三种脐橙共
三种脐橙共![]() 吨到外地销售.按计划,
吨到外地销售.按计划,![]() 辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
脐橙品种 |
|
|
|
每辆汽车运载量(吨) |
|
|
|
每吨脐橙获得(元) |
|
|
|
![]() 设装运
设装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,装运
,装运![]() 种脐橙的车辆数为
种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如果装运每种脐橙的车辆数都不少于
如果装运每种脐橙的车辆数都不少于![]() 辆,那么车辆的安排方案有几种?
辆,那么车辆的安排方案有几种?
![]() 设销售利润为
设销售利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形![]() 的顶点
的顶点![]() 、
、![]() 在反比例函数
在反比例函数![]() 图像上,
图像上,![]() ,上底边
,上底边![]() 在直线
在直线![]() 上,下底边
上,下底边![]() 交
交![]() 轴于
轴于![]() ,点
,点![]() 的纵坐标是1.
的纵坐标是1.
(1)求反比例函数的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,其他条件不变,探究四边形
,其他条件不变,探究四边形![]() 的面积;
的面积;
(4)若将点![]() 的坐标改为
的坐标改为![]() ,且
,且![]() ,点
,点![]() 的纵坐标改为
的纵坐标改为![]() ,且
,且![]() ,其他条件不变,直接写出四边形
,其他条件不变,直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)求△A2B2C2面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】豫让桥豫东市场某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个.若销售单价每个降低2元,则每周可多卖出20个;若商户计划下周利润达到5200元,则此电子产品的售价为每个多少元?设销售价格每个降低x元(x为偶数),则所列方程为( )
A. (80﹣x)(160+20x)=5200 B. (30﹣x)(160+20x)=5200
C. (30﹣x)(160+10x)=5200 D. (50﹣x)(160+10x)=5200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com