
【题目】如图,在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,则DE的长是__________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC, ∠A=40°,O为边BC的中点,把△ABC绕O顺时针旋转m(0<m<180)度后,如果点B恰好落在初始△ABC的边上,那么m=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
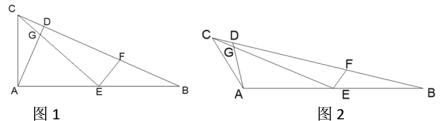
【题目】如图,在△ABC中,AB=2AC, 点D在BC上,且∠CAD=∠B,点E是AB的中点,联结CE与AD交于点G,点F在BC上,且∠CEF=∠BAC.
(1)若∠BAC=90°,如图1,求证: EG+ EF=![]() AC;
AC;
(2)若∠BAC=120°,如图2,请猜想线段EG,EF和AC之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)当![]() __________时,
__________时,![]() 有意义;(2)当
有意义;(2)当![]() __________时,
__________时,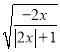 有意义;
有意义;
(3)当__________时,![]() 有意义;(4)当
有意义;(4)当![]() __________时,
__________时,![]() 有意义.
有意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
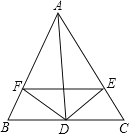
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
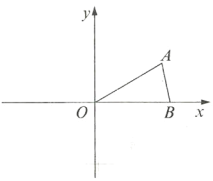
【题目】已知等腰![]() 在平面直角坐标系中的位置如图,点
在平面直角坐标系中的位置如图,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
(1)若将![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位,此时点
个单位,此时点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(2)若将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(3)若将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() 到
到![]() 位置,当点
位置,当点![]() 、
、![]() 恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点
恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点![]() 、
、![]() 且以
且以![]() 轴为对称的抛物线解析式.
轴为对称的抛物线解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com