
【题目】(1)当![]() __________时,
__________时,![]() 有意义;(2)当
有意义;(2)当![]() __________时,
__________时,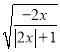 有意义;
有意义;
(3)当__________时,![]() 有意义;(4)当
有意义;(4)当![]() __________时,
__________时,![]() 有意义.
有意义.
【答案】(1)![]() , (2)
, (2)![]() , (3)
, (3)![]() (4)
(4)![]() 且
且![]()
【解析】
(1)根据二次根式有意义则被开方数大于等于0,且分母不为0,列式求解;(2)根据二次根式有意义则被开方数大于等于0,且分母不为0,结合绝对值是非负数,列式求解;(3)根据二次根式有意义则被开方数大于等于0,列式求解;(4)根据二次根式有意义则被开方数大于等于0,且分母不为0,列式求解.
解:(1)∵式子 ![]() 有意义,
有意义,
∴![]() ,且
,且![]()
∴![]()
∴当![]() 时,
时,![]() 有意义;
有意义;
(2)∵式子 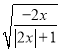 有意义,
有意义,
∴![]() ,且
,且![]()
∴![]()
∴当![]() 时,
时,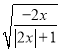 有意义;
有意义;
(3)∵式子 ![]() 有意义,
有意义,
∴![]() ,
,
∴![]()
∴当![]() 时,
时,![]() 有意义;
有意义;
(4)∵式子 ![]() 有意义,
有意义,
∴![]() ,且
,且![]()
∴![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() 时,
时,![]() 有意义.
有意义.
故答案为:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,且
,且![]()


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=![]() (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
(k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )

A. 5 B. 10 C. 15 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)求△A2B2C2面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】豫让桥豫东市场某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个.若销售单价每个降低2元,则每周可多卖出20个;若商户计划下周利润达到5200元,则此电子产品的售价为每个多少元?设销售价格每个降低x元(x为偶数),则所列方程为( )
A. (80﹣x)(160+20x)=5200 B. (30﹣x)(160+20x)=5200
C. (30﹣x)(160+10x)=5200 D. (50﹣x)(160+10x)=5200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“建设社会主义新农村”工作组到某乡大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备,其费用p(万元)与大棚面积x(公顷)的函数关系式为p=0.9x2;另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.若某菜农期望通过种植大棚蔬菜当年获得5万元收益(扣除修建和种植成本后),从投入的角度考虑应建议他修建多少公项大棚?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知P是半径为5cm的⊙O内一点.解答下列问题:

(1)用尺规作图找出圆心O的位置.(要求:保留所有的作图痕迹,不写作法)
(2)用三角板分别画出过点P的最长弦AB和最短弦CD.
(3)已知OP=3cm,过点P的弦中,长度为整数的弦共有 _________ 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,EF是长为8的弦,OG⊥EF于点G,点A在GO的延长线上,且AO=13.弦EF从图1的位置开始绕点O逆时针旋转,在旋转过程中始终保持OG⊥EF,如图2.
[发现]在旋转过程中,
(1)AG的最小值是 ,最大值是 .
(2)当EF∥AO时,旋转角α= .
[探究]若EF绕点O逆时针旋转120°,如图3,求AG的长.
[拓展]如图4,当AE切⊙O于点E,AG交EO于点C,GH⊥AE于H.
(1)求AE的长.
(2)此时EH= ,EC= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com