
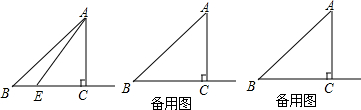
分析 (1)由线段垂直平分线的性质可知AE=BE=x,然后再在Rt△AEC中,依据勾股定理列方程求解即可;
(2)先由勾股定理求得AB=10,由翻折的性质求得BC′=4,C′E=8-x,在Rt△BEC′中,依据勾股定理列方程求解即可.
解答 解:(1)设BE=x,则EC=8-x.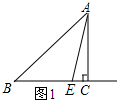
∵点E在AB的垂直平分线上,
∴AE=BE=x.
在Rt△AEC中,AE2=EC2+AC2,即x2=(8-x)2+62.
解得:x=$\frac{25}{4}$.
(2)如图2所示.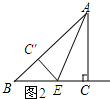
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10.
由翻折的性质可知:∠C=∠AC′E=90°,AC′=AC=6,EC=EC′.
在Rt△BEC′中,由勾股定理得:BE2=C′B2+C′E2,即x2=42+(8-x)2,
解得:x=5.
点评 本题主要考查的是翻折的性质、勾股定理、线段垂直平分线的性质,掌握翻折的性质、勾股定理、线段垂直平分线的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.2×108 | B. | 7.2×109 | C. | 7.2×1010 | D. | 7.2×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
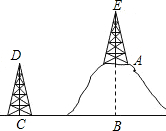 如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?
如图,小山高AB=75米,B,C两点间的水平距离为40米,两铁塔的高相等,即CD=AE.如果要在两铁塔顶D,E间架设一条高压线,那么这条高压线至少为多长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com