
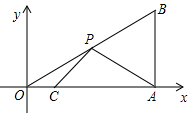
 如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.
如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$. 分析 作出点C关于OP的对称点C′,然后由轴对称的性质和特殊锐角三角函数,求得点C′的坐标,最后根据两点间的距离公式求得C′A的长度,从而求得PC+PA的最小值.
解答 解:如图所示:作出点C关于OP的对称点C′.
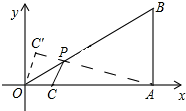
∵点B的坐标为(3,$\sqrt{3}$),
∴tan∠BOA=$\frac{\sqrt{3}}{3}$.
∴∠BOA=30°.
由轴对称的性质可知:OC=OC′=1,∠C′OP=∠COP=30°,
∴sin60°×OC′=$\frac{\sqrt{3}}{2}×1=\frac{\sqrt{3}}{2}$,cos60°×OC′=$\frac{1}{2}×1$=$\frac{1}{2}$.
∴点C′的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
由两点间的距离公式可知:C′A=$\sqrt{(3-\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2}-0)^{2}}$=$\sqrt{7}$.
由两点之间线段最短可知;当C′、P、A在一条直线上时,点PA+PC′有最小值
∴PA+PC的最小值=PA+PC′=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题主要考查的是轴对称的性质、特殊锐角三角函数、勾股定理,明确当C′、P、A在一条直线上时,点PA+PC′有最小值是解题的关键.


科目:初中数学 来源: 题型:解答题
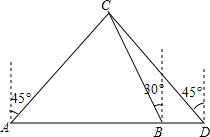 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2=0 | B. | x2=1 | C. | x2=-2 | D. | x2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )
如图,是一个机器零件的设计图纸(单位:mm),根据图纸中的数据L=40±0.02,用不等式表示合格率零件的长度L的取值范围是( )| A. | L≤40.2 | B. | L≥39.98 | C. | 39.98≤L≤40.02 | D. | 39.8≤L≤40.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
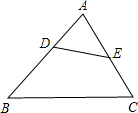 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
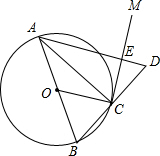 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com