
【题目】如图,已知抛物线y=﹣x2+2x+3与坐标轴交于A,B,C三点,抛物线上的点D与点C关于它的对称轴对称.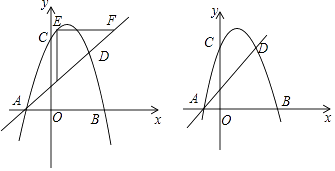
(1)直接写出点D的坐标和直线AD的解析式;
(2)点E是抛物线上位于直线AD上方的动点,过点E分别作EF∥x轴,EG∥y轴并交直线AD于点F、G,求△EFG周长的最大值;
(3)若点P为y轴上的动点,则在抛物线上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标,若不存在,请说明理由.
【答案】
(1)
解:将x=0代入得y=3,
∴C(0,3).
∵抛物线的对称轴为x=﹣ ![]() =1,C(0,3),
=1,C(0,3),
∴D(2,3).
把y=0代入抛物线的解析式得:0=﹣x2+2x+3,解得x=3或x=﹣1,
∴A(﹣1,0).
设直线AD的解析式为y=kx+b,将点A和点D的坐标代入得: ![]() ,解得:k=1,b=1,
,解得:k=1,b=1,
∴直线AD的解析式为y=x+1.
(2)
解:如图1所示:
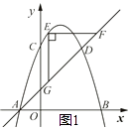
∵直线AD的解析式为y=x+1,
∴∠DAB=45°.
∵EF∥x轴,EG∥y轴,
∴∠GEF=90°,∠GFE=∠DAB=45°
∴△EFG是等腰直角三角形.
∴△EFG的周长=EF+FG+EG=(2+ ![]() )EG.
)EG.
依题意,设E(t,﹣t2+2t+3),则G(t,t+1).
∴EG=﹣t2+2t+3﹣(t+1)=﹣(t﹣ ![]() )2+
)2+ ![]() .
.
∴EG的最大值为 ![]() .
.
∴△EFG的周长的最大值为 ![]() +
+ ![]() .
.
(3)
解:存在.①以AD为平行四边形的边时,PQ∥AD,PQ=AD.
∵A,D两点间的水平距离为3,
∴P,Q两点间的水平距离也为3.
∴点Q的横坐标为3或﹣3.
将x=3和x=﹣3分别代入y=﹣x2+2x+3得y=0或y=﹣12.
∴Q(3,0)或(﹣3,﹣12).
②当AD为平行四边形的对角线时,设AD的中点为M,
∵A(﹣1,0),D(2,3),M为AD的中点,
∴M( ![]() ,
, ![]() ).
).
设点Q的横坐标为x,则 ![]() =
= ![]() ,解得x=1,
,解得x=1,
∴点Q的横坐标为1.
将x=1代入y=﹣x2+2x+3得y=4.
∴这时点Q的坐标为(1,4).
综上所述,当点Q的坐标为Q(3,0)或(﹣3,﹣12)或(1,4)时,以A,D,P,Q为顶点的四边形是平行四边形.
【解析】(1)先求得点C的坐标,然后再求得抛物线的对称轴,由点C与点D关于x=1对称可求得点D的坐标,把y=0代入抛物线的解析式可求得对应的x的值,从而可得到点A的坐标,然后利用待定系数法求得直线AD的解析式即可;(2)首先证明△EFG为等腰直角三角形,则△EFG的周长=(2+ ![]() )EG,设E(t,﹣t2+2t+3),则G(t,t+1),然后得到EG与t的函数关系式,利用配方法可求得EG的最大值,最后依据△EFG的周长=(2+
)EG,设E(t,﹣t2+2t+3),则G(t,t+1),然后得到EG与t的函数关系式,利用配方法可求得EG的最大值,最后依据△EFG的周长=(2+ ![]() )EG求解即可;(3)分为AD为平行四边形的边和AD为平行四边形的对角线时,两种情况,可先利用平行四边形的性质求得点Q的横坐标,然后将点Q的横坐标代入抛物线的解析式可求得点Q的纵坐标.
)EG求解即可;(3)分为AD为平行四边形的边和AD为平行四边形的对角线时,两种情况,可先利用平行四边形的性质求得点Q的横坐标,然后将点Q的横坐标代入抛物线的解析式可求得点Q的纵坐标.


科目:初中数学 来源: 题型:
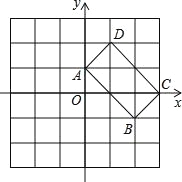
【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市新建火车站广场将投入使用,计划在广场内种植A,B两种花木共4000棵,若A花木数量是B花木数量的2倍还多400棵.
(1)求A,B两种花木的数量分别是多少棵?
(2)如果园林处安排24人同时种植这两种花木,每人每天能种植A花木70棵或B花木60棵,应怎样分别安排种植A花木和种植B花木的人数,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路:一条是全长400千米的普通公路,一条是全长360千米的高速公路.某客车在高速公路上行驶的平均速度比在普通公路上行驶的平均速度快50千米/时,从甲地到乙地由高速公路上行驶所需的时间比普通公路上行驶所需的时间少6小时.求该客车在高速公路上行驶的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式 12=1= ![]() ×1×2×(2+1)
×1×2×(2+1)
12+22= ![]() ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ![]() ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ![]() ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73) 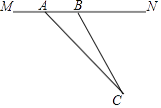
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A. 商贩A的单价大于商贩B的单价
B. 商贩A的单价等于商贩B的单价
C. 商版A的单价小于商贩B的单价
D. 赔钱与商贩A、商贩B的单价无关
查看答案和解析>>
科目:初中数学 来源: 题型:
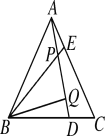
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com