
����Ŀ��ij�̳�Ҫ��һ������ͣ������ͣ������������ʾ��ͼ��ͼ��ʾ������б�µ���б��Ϊ18����һ¥������ͣ��������ľ���CD��2.8�ף�һ¥����ƽ�ߵľ���BC��1�ף�
(1)Ϊ��֤б�µ���б��Ϊ18����Ӧ�ڵ����Ͼ��B��Զ��A����ʼб�µ�ʩ����(�����ȷ��0.1��)
(2)��������̳��ͻ��Ļ����߶�Ϊ2.5�ף���ô������������ܷ�֤����˳���������ͣ��������˵�����ɣ�(�ο����ݣ�sin 18���0.31��cos 18���0.95��tan 18���0.32)

���𰸡���1��5.6������2���ܣ����ɼ�����
����������1��������ɵá�BAD=18�㣬BD=CD-CB=1.8���ף���Ȼ����Rt��ABD�У������Ǻ��������ʣ��������AB�ij���
��2�����ȹ�C��CE��AD������ΪE������á�DCE�Ķ�����Ȼ����Rt��CDE�У������Ǻ��������ʼ��ɵ�CE=CDcos18�����̶���ô𰸣�
�⣺(1)������ɵá�BAD��18��.��Rt��ABD�У�AB��![]() ��
��![]() ��5.6(��)
��5.6(��)
��Ӧ�ڵ����Ͼ�B��5.6��Զ��A����ʼб�µ�ʩ��
(2)��.���ɣ���ͼ������C��CE��AD�ڵ�E��
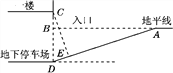
���DCE����BAD��18��.��Rt��CED��CE��CD��cos 18���2.8��0.95��2.66(��).
��2.66��2.5��
���ܱ�֤����˳���������ͣ������


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ���������С���ھ��꼶�����ȡ��һ����ѧ������ĩ��ѧ�ɼ�Ϊ��������ΪA��100��90�֣���B��89��80�֣���C��79��60�֣���D��59��0�֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
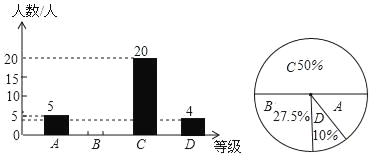
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ��1200�ˣ�������Ϊ80�֣���80�֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʵ�Ա��Ħ�г����ʾֳ���������������2km����A�壬������������3km����B �壬Ȼ��������9km��C�壬���ص��ʾ�.
(1)���ʾ�Ϊԭ�㣬������Ϊ��������1����λ���ȱ�ʾ1km�������������ϱ�ʾ��A��B��C������ׯ��λ�ã�
![]()
(2)C����A���ж�Զ��
(3)��Ħ�г�ÿ100km����3��������·�����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���µ�Ƽ�����˾��160��Ԫ����Ϊ�²�Ʒ���з����ã��ɹ����Ƴ���һ���г�����ĵ��Ӳ�Ʒ�����ڵ���Ͷ���������������ۣ���֪�������ֵ��Ӳ�Ʒ�ijɱ�Ϊ4Ԫ/���������۹����з��֣�ÿ�����������y������������ۼ۸�x��Ԫ/�����Ĺ�ϵ��ͼ��ʾ������ABΪ����������ͼ���һ���֣�BCΪһ�κ���ͼ���һ���֣��蹫˾�������ֵ��Ӳ�Ʒ��������Ϊs����Ԫ������ע������һ��ӯ������ӯ����������һ�������������һ���������������һ��ijɱ�����
��1�������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2�������һ�����ֵ��Ӳ�Ʒ��������s����Ԫ����x��Ԫ/����֮��ĺ�����ϵʽ���������һ������������ֵ��
��3�����蹫˾�����ֵ��Ӳ�Ʒ��һ��ǡ�ð�������s����Ԫ��ȡ�����ֵʱ�������ۣ��ָ��ݵ�һ���ӯ������������ڶ��꽫���ֵ��Ӳ�Ʒÿ�������ۼ۸�x��Ԫ������8Ԫ���ϣ�x��8�������ڶ������������103��Ԫʱ������������s����Ԫ�������ۼ۸�x��Ԫ/�����ĺ���ʾ��ͼ�������ۼ۸�x��Ԫ/������ȡֵ��Χ��
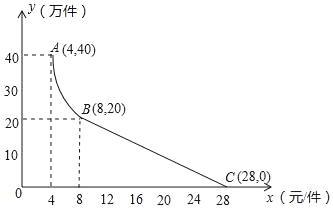
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�ı��Ϊ500Ԫ/�����������ν��ۺ�ļ۸�Ϊ320Ԫ/�����������ν��۵İٷ�����ͬ.
��1���������Ʒÿ�ν��۵İٷ��ʣ�
��2��������Ʒ����Ϊ280Ԫ/�������ν��۹��۴�����Ʒ100����Ϊʹ���ν������۵�����������8000Ԫ�����һ�ν��ۺ�����Ҫ�۳�������Ʒ���ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���������ABC�У�AB=AC����D��BA���ӳ����ϣ�BC=24�� ![]() ��
��
��1����AB�ij���
��2����AD=6.5����![]() ������ֵ��
������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУҪ�Ӽ�����������˶�Ա����ѡһ�˲μ�ȫ�б�������ѡ�����У�ÿ�˽�����5��������ijɼ�������Ϊ��9.7��10��9.6��9.8��9.9���ҵijɼ���ƽ����Ϊ9.8������Ϊ0.032��
��1��������ɼ���ƽ�����ͷ���ֱ��Ƕ��٣�
��2���ݹ��ƣ�����ɼ���ƽ�����ﵽ9.8���Ϳ��ܶ�ý��ƣ�Ϊ�˶�ý��ƣ�Ӧѡ˭�μӱ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��֯���չ�ij����ɫ������ֱ��ת��������ɫ������ÿ�ֿɻ�õ�����Ϊ500Ԫ.������![]() ���ӹ���ת������ÿ�ֿɻ�õ�����Ϊ1000Ԫ��������
���ӹ���ת������ÿ�ֿɻ�õ�����Ϊ1000Ԫ��������![]() ���ӹ���ת������ÿ�ֿɻ�õ�����Ϊ2000Ԫ.��֪�÷�֯����������
���ӹ���ת������ÿ�ֿɻ�õ�����Ϊ2000Ԫ.��֪�÷�֯����������![]() ���ӹ���ÿ��ɼӹ�16�֣�����
���ӹ���ÿ��ɼӹ�16�֣�����![]() ���ӹ���ÿ��ɼӹ�6�֣��������ֵȼ��ļӹ�����ͬʱ����.���÷�֯���չ���140��������ɫ��������15���ڼӹ��꣬�����������ֿ��з�����
���ӹ���ÿ��ɼӹ�6�֣��������ֵȼ��ļӹ�����ͬʱ����.���÷�֯���չ���140��������ɫ��������15���ڼӹ��꣬�����������ֿ��з�����
����һ�������չ�����ɫ��ֱ��ת��.
���������������ܶ����ɫ������![]() ���ӹ������µIJ���ֱ��ת��.
���ӹ������µIJ���ֱ��ת��.
��������һ���ֽ���![]() ���ӹ�����һ���ֽ���
���ӹ�����һ���ֽ���![]() ���ӹ���ǡ��15�����.
���ӹ���ǡ��15�����.
�����Ǹ÷�֯�������ˣ���Ҫ������࣬�����ʹ������������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com