
 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.分析 (1)通过证明△BOE≌△COF得到∠B=∠C,进而得出结论;
(2)通过证明△BOE≌△COF得到∠OBE=∠OCF,由于OB=OC,得到∠OBC=∠OCB,于是得到∠ABC=∠ACB,于是得的结论;
(3)过点O作OE、OF分别与AB、AC垂直于点E、F,连接OB、OC,首先证明△BOE≌△COF,得到∠ABO=∠ACO,由OB=OC根据等边对等角得∠OBC=∠OCB,进而得到∠ABC=∠ACB,从而得出结论:AB=AC.
解答 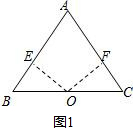 解:(1)证明:如图1,过点O作OE、OF分别与AB、AC垂直于点E、F,
解:(1)证明:如图1,过点O作OE、OF分别与AB、AC垂直于点E、F,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△BOE与Rt△COF中$\left\{\begin{array}{l}{OE=OF}\\{OB=OC}\end{array}\right.$,
∴Rt△BOE≌Rt△COF,
∴∠B=∠C,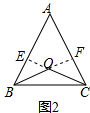
∴AB=AC;
(2)证明:如图2,过点O作OE、OF分别与AB、AC垂直于点E、F,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△BOE与Rt△COF中$\left\{\begin{array}{l}{OE=OF}\\{OB=OC}\end{array}\right.$,
∴Rt△BOE≌Rt△COF,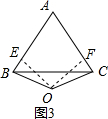
∴∠OBE=∠OCF,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)不一定成立,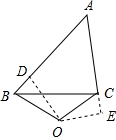
如图3,证明:过点O作OE、OF分别与AB、AC垂直于点E、F,连接OB、OC,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
又∵OB=OC,
∴△BOE≌△COF(HL),
∴∠ABO=∠ACO,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABO-∠OBC=∠ACO-∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
如图4,此题不成立.
点评 本题考查了全等三角形的判定及其性质、等腰三角形的判定等知识;正确作出辅助线是解答本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
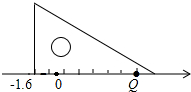 慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.
慧慧自己做了一个三角形的纸片,并在其中的一边画了七个长度相等的小格,每小格的长度为1个单位长度,然后把此边放在如图所示的数轴上,则点Q所表示的数是5.4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
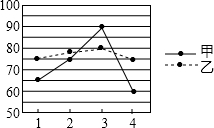 如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )
如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )| A. | 甲成绩比乙成绩稳定 | B. | 乙成绩比甲成绩稳定 | ||
| C. | 甲、乙两成绩一样稳定 | D. | 不能比较两人成绩的稳定性 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8个 | B. | 9个 | C. | 10个 | D. | 11个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com