
| A. | 8个 | B. | 9个 | C. | 10个 | D. | 11个 |
分析 根据已知得出(a-b)2+(b-c)2+(a-c)2=26①,令a-b=m,b-c=n,则a-c=m+n,代入可得出符合条件的m和n的值的组合,分别代入讨论,根据b+c>a可得出c的最小范围,根据周长不超过30可得出c的最大值范围,进而可得出符合题意的三角形的个数.
解答 解:∵a2+b2+c2-ab-ac-bc=13,
∴(a-b)2+(b-c)2+(a-c)2=26 ①,
令a-b=m,b-c=n,则a-c=m+n,其中m,n均为自然数,
于是,等式①变为m2+n2+(m+n)2=26,即m2+n2+mn=13 ②
由于m,n均为自然数,判断易知,使得等式②成立的m,n只有两组:
$\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$和$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$
(1)当m=3,n=1时,b=c+1,a=b+3=c+4.
又a,b,c为三角形的三边长,所以b+c>a,即(c+1)+c>c+4,解得c>3.
又因为三角形的周长不超过30,
即a+b+c=(c+4)+(c+1)+c≤30,
解得c≤$\frac{25}{3}$,因此3<c≤$\frac{25}{3}$,
所以c可以取值4,5,6,7,8,对应可得到5个符合条件的三角形.
(2)当m=1,n=3时,b=c+3,a=b+1=c+4.又a,b,c为三角形的三边长,
所以b+c>a,即(c+3)+c>c+4,
解得c>1.
又因为三角形的周长不超过30,
即a+b+c=(c+4)+(c+3)+c≤30,解得.
因此c≤$\frac{23}{3}$,因此1<c≤$\frac{23}{3}$,
所以c可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形.
综合可知:符合条件且周长不超过30的三角形的个数为5+6=11.
故选:D.
点评 本题考查了因式分解的运用,三角形的三边关系,难度较大,解答本题首先是将a2+b2+c2-ab-ac-bc=13进行变形,根据a-b=m,b-c=n,a-c=m+n得出符合题意的m、n的值的组合是解答本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
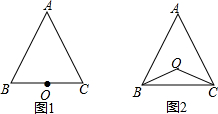 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com