
����Ŀ����һ�����������![]() �������
�������![]() ���������dz���ɫ�������ͬ��
���������dz���ɫ�������ͬ��
![]() �ж����м������˵�˵������Ϊ�Ե��ں��������ڴ����̡������Ĵ���
�ж����м������˵�˵������Ϊ�Ե��ں��������ڴ����̡������Ĵ���![]() ����
����
�ף���������������һ�����ǰ�����ߺ�������һ�¼��DZ�Ȼ�¼�________��
�ң�������������һ��������ɫ��Żأ����ȣ����������������Σ����б���һ���������ǰ���________��
![]() С��˵��������������һ�����Żأ�������һ�������������������а�������һ�¼��ĸ���Ϊ
С��˵��������������һ�����Żأ�������һ�������������������а�������һ�¼��ĸ���Ϊ![]() ������ͬ���뻭��״ͼ���б�����˵����
������ͬ���뻭��״ͼ���б�����˵����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ʻʱ�ĺ�����Ϊ0.1��/ǧ�ף���ͼ������ʣ������![]() ���������ڼ����ͺ�����ʻ��·��
���������ڼ����ͺ�����ʻ��·��![]() ��ǧ�ף��ĺ���ͼ��.
��ǧ�ף��ĺ���ͼ��.

��1������ͼ��ֱ��д��������ʻ400ǧ��ʱ�������ڵ�ʣ�������������������ʱ�����������
��2����![]() ����
����![]() �ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�ĺ�����ϵʽ���������������ʣ������5��ʱ������ʻ��·��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�������1�������2��������Щ�����ɫ�ⶼ��ͬ�����Ⱥ������������1����¼��ɫ��Żأ����ȣ��ٴ�����������1�����������зŻص��Ⱥ�����2��.���������2�֣����������1��.
(1)��һ����������ĸ����Ƕ���?
(2)�������������ܷ�Ϊ4�ֵĸ����Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015��
�1����һֻ�����Ŀڴ���װ�б��Ϊ1��2��3��3��С����Щ�������ⶼ��ͬ����ֽ��ȣ��ס��ҡ�����λͬѧ���������ҵ�˳�����δӴ��и�����һ�����Żأ�������1����ʤ���������ʤ���ĸ��ʣ���ע�����������ұ�ʾ����һ�����ڶ������������һ������
�2����һֻ�����Ŀڴ���װ�б��Ϊ1��2��3��4��4��С����Щ�������ⶼ��ͬ����ֽ��ȣ�����Լס��ҡ�������ͬѧ�涨һ������˳�� �� �� �����ǰ����˳��Ӵ��и�����һ�����Żأ�������1����ʤ�������һ�������ͬѧʤ���ĸ��ʵ��� �����һ�������ͬѧʤ���ĸ��ʵ��� ��
���룺��һֻ�����Ŀڴ���װ�б��Ϊ1��2��3������n��nΪ����������n��С����Щ�������ⶼ��ͬ����ֽ��ȣ��ס��ҡ�������ͬѧ�Ӵ��и�����һ�����Żأ�������1����ʤ�������룺������ͬѧÿ��ʤ���ĸ���֮��Ĵ�С��ϵ��
�㻹�ܵõ�ʲô����飿��д��һ�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��ӯ��45Ԫ��Ϊ���������ۡ�����ӯ��������ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ������ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�4�������̳�ƽ��ÿ��ӯ��2100Ԫ��ÿ������Ӧ���۶���Ԫ��������������⣺
��1��δ����֮ǰ��ij�̳���������ӯ��Ϊ�� �� Ԫ��
��2�����ۺ���ij�̳�ÿ������Ӧ����xԪ����ÿ������ӯ���� ��Ԫ��ƽ��ÿ����۳��� �������ú�x�Ĵ���ʽ���б�ʾ��
��3�����г����̣����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ���
�⣺��x2��4x��y��
ԭʽ����y+2����y+6��+4������һ����
��y2+8y+16�����ڶ�����
����y+4��2����������
����x2��4x+4��2�����IJ���
��1����ͬѧ�ڶ�������������������ʽ�ֽ���� ��������ţ���
A����ȡ����ʽ B��ƽ���ʽ
C�������͵���ȫƽ����ʽ D�����������ȫƽ����ʽ
��2����ͬѧ�ڵ��IJ���y�������е�x�Ĵ���ʽ�������õ���ʽ�ֽ����������������Ƿ�ֽ����� �����������������������������ֱ��д�����Ľ���� ����
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC����AB=AC����D��BC���е㣬��E��AD�ϣ�����BE��CE.
(1)��֤��BE=CE
(2)��ͼ2����BE���ӳ��߽�AC�ڵ�F����BF ��AC������ΪF��ԭ���������������䣮��֤����CAD=��CBF
(3)��(2)�������£�����BAC=45![]() ���жϡ�CFE����״����˵�����ɣ�
���жϡ�CFE����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ACB�У���ACB=90�㣬��ABC��ƽ����BE����BAC�����ƽ����AD�ཻ�ڵ�P���ֱ�AC��BC���ӳ�����E��D����P��PF��AD��AC���ӳ����ڵ�H����BC���ӳ����ڵ�F������AF��DH�ڵ�G�������н��ۣ��١�APB=45�㣻��PF=PA����BD��AH=AB����DG=AP+GH��������ȷ���ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
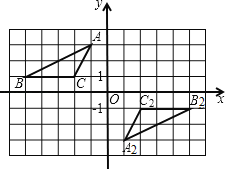
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A(��1��3)��B(��5��1)��C(��2��1).
(1)��ABC�����Ϊ______.
(2)��ͼ��������ABC����x��ĶԳ�ͼ�Ρ�A1B1C1����д����A1������.
(3)��˵����A2B2C2���ɡ�A1B1C1���������ı任�õ��ģ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com