
【题目】已知:在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在对角线
在对角线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,
,![]() 的延长线与射线
的延长线与射线![]() 交于点
交于点![]() ,设
,设![]() 的长为
的长为![]() .
.
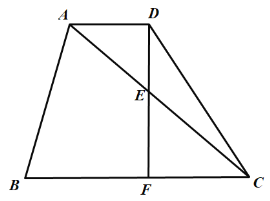
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
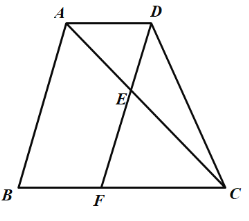
(2)设![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并直接写出定义域;
的函数解析式,并直接写出定义域;
(3)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() 且
且![]() );(3)当
);(3)当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长是6或
的长是6或![]() .
.
【解析】
(1)过![]() 作
作![]() ,利用
,利用![]() 求出CH,根据勾股定理求出AH,再证明四边形
求出CH,根据勾股定理求出AH,再证明四边形![]() 是矩形,得到
是矩形,得到![]() ,再根据
,再根据![]() ,
,![]() 求出
求出![]() ,从而求出AD;
,从而求出AD;
(2)根据题意证明![]() ,得到
,得到![]() ,故
,故![]() ,在
,在![]() 中,利用勾股定理得到
中,利用勾股定理得到![]() 故得到
故得到![]() ,即可得到
,即可得到![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)先证明![]() ,再分DF=DC、FC=DC、FC=FD三种情况,根据y与x的函数关系与三角函数的定义求解即可.
,再分DF=DC、FC=DC、FC=FD三种情况,根据y与x的函数关系与三角函数的定义求解即可.
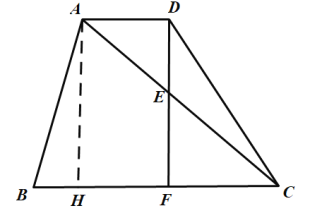
解:(1)过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵在![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]()
∴在![]() 中,
中,![]() ,
,
∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]()
∵在![]() 中,
中,![]() ,且
,且![]()
∴![]() ,得:
,得:![]()
∴![]()
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵在![]() 中,
中,![]()
∴![]() ,即
,即![]() (
(![]() 且
且![]() )
)
(3)由![]() ,
,![]() 得:
得:![]() ,
,
又![]() 有
有![]() ,
,
∴![]()
∴当![]() 是等腰三角形时,
是等腰三角形时,![]() 也是等腰三角形
也是等腰三角形
∴1°当![]() 时,不存在;
时,不存在;
2°当![]() 时,得:
时,得:![]() ,即
,即![]()
解得:![]() (舍),
(舍),![]()
3°当![]() 时,在
时,在![]() 中由
中由![]()
得: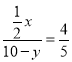 ,解得:
,解得:![]() (舍),
(舍),![]()
∴综上所述,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长是6或
的长是6或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -2 | -2 | 0 | 4 | … |
(1)求该二次函数的表达式;
(2)当y≥4时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
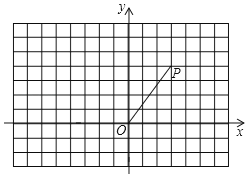
【题目】如图,在平面直角坐标系中,点P(3,4),连接OP,将线段OP绕点O逆时针旋转90°得线段OP1.
(1)在图中作出线段OP1,并写出P1点的坐标;
(2)求点P在旋转过程中所绕过的路径长;
(3)求线段OP在旋转过程中所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
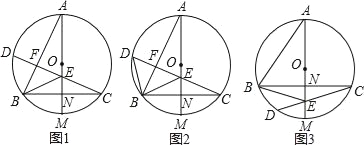
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com