
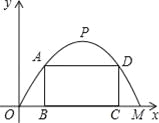
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.
【答案】(1)M(12,0),P(6,6);(2)y=![]() x2+2x;(3)15米.
x2+2x;(3)15米.
【解析】试题分析:确定了抛物线的顶点式,可以设抛物线的顶点式,又过原点(0,0),就可以确定抛物线解析式;设OB=x,由对称性得CM=x,这样就可以用含x的式子表示AB、AD、CD了,为求三根木杆AB、AD、DC的长度之和的最大值,提供依据.
试题解析:(1)M(12,0),P(6,6)
(2)∵顶点坐标(6,6)
∴设y=a(x﹣6)2+6(a≠0)
又∵图象经过(0,0)
∴0=a(0﹣6)2+6
∴a=![]()
∴这条抛物线的函数解析式为y=![]() (x﹣6)2+6,即y=
(x﹣6)2+6,即y=![]() x2+2x;
x2+2x;
(3)设A(x,y)
∴A(x, ![]() (x﹣6)2+6)
(x﹣6)2+6)
∵四边形ABCD是矩形,
∴AB=DC=![]() (x﹣6)2+6,
(x﹣6)2+6,
根据抛物线的轴对称性,可得:OB=CM=x,
∴BC=12﹣2x,即AD=12﹣2x,
∴令L=AB+AD+DC=2[![]() (x﹣6)2+6]+12﹣2x=
(x﹣6)2+6]+12﹣2x=![]() x2+2x+12=
x2+2x+12=![]() (x﹣3)2+15.
(x﹣3)2+15.
∴当x=3,L最大值为15
∴AB、AD、DC的长度之和最大值为15米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=8,∠BAC=30°.将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处.延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,2016年某县投入教育经费6000万元,2018年投入教育经费8640万元,假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2019年该县投入教育经费多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
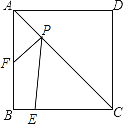
【题目】如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( ).
A.5B.![]() C.
C.![]() D.无法确定
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
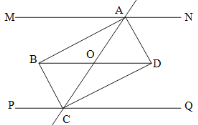
【题目】如图所示,已知直线MN//PQ,直线AC交MN、PQ于点A、C,所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.试猜想AC与BD的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上对应点如图所示,且|a|>|b|.
![]()
(1)|a﹣b|= ,|a+b|= ,|a+c|= ,|b﹣c|= ;
(2)化简|a﹣b|﹣|a+b|+|a+c|﹣|b﹣c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,则下列结论中错误的是( )
![]()
A. a+c<0B. -a+b+c<0
C. |a+b|>|a+c|D. |a+b|<|a+c|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com