
【题目】一张长方形纸片的长为m,宽为n(m>3n)如图1,先在其两端分别折出两个正方形(ABEF、CDGH)后展开(如图2),再分别将长方形ABHG、CDFE对折,折痕分别为MN、PQ(如图3),则长方形MNQP的面积为( )

A.n2B.n(m﹣n)C.n(m﹣2n)D.![]()
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】我们约定:64 2 2 2 2 2 2可表示成f (6)64,也可表示成g(64)6,
(1)求:f (8) ;
(2)求:g(512);
(3)求:gf (x) (x 为正整数);
(4)f (x y) f (x) f ( y)(x,y 是正整数)成立吗?为什么?
(5)x,y 分别表示若干个2相乘的积,类比④你能写出与 g 相关的等式吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:![]() 。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
。当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:![]() 。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如:
。假分式可以化为整式与真分式和的形式,我们也称之为带分式,如:![]() 。
。
解决问题:
(1)下列分式中属于真分式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)将假分式![]() 分别化为带分式;
分别化为带分式;
(3)若假分式![]() 的值为整数,请直接写出所有符合条件的整数x的值。
的值为整数,请直接写出所有符合条件的整数x的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种树苗,第一次分别购进A、B两种树苗30棵和15棵,共花费675元;第二次分别购进A、B两种树苗12棵和5棵,共花费265元.两次购进的A、B两种树苗价格均分别相同.
(1)A、B两种树苗每棵的价格分别是多少元?
解:设A种树苗每棵x元,B种树苗每棵y元
根据题意列方程组,得: ;
解这个方程组,得: ;
答: .
(2)若购买A、B两种树苗共31棵,且购买树苗的总费用不超过320元,则最多可以购买A种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动;同时动点
运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,运动时间是
运动,运动时间是![]() 秒.
秒.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度.
的长度.
(2)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 位于线段
位于线段![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(4)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,ABCD中,BE,CF分别是∠ABC和∠BCD的角平分线,BE,CF相交于点O.
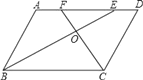
(1)求证:BE⊥CF;
(2)试判断AF与DE有何数量关系,并说明理由;
(3)当△BOC为等腰直角三角形时,四边形ABCD是何特殊四边形?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人购进一批琼中绿橙到市场上零售,已知卖出的绿橙数量x(千克)与售价y(元)的关系如下表:
数量x(千克) | 1 | 2 | 3 | 4 | 5 | … |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 | … |
(1)写出售价y(元)与绿橙数量x(千克)之间的函数关系式;
(2)这个人若卖出50千克的绿橙,售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,正方形
,正方形![]() 的点
的点![]() 在线段
在线段![]() 上,点
上,点![]() ,
,![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() .将正方形
.将正方形![]() 沿
沿![]() 轴正方向平移,得到正方形
轴正方向平移,得到正方形![]() ,当点
,当点![]() 与点
与点![]() 重合时停止运动.设平移的距离为
重合时停止运动.设平移的距离为![]() ,正方形
,正方形![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() .
.
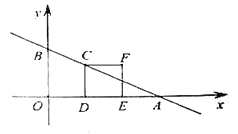
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 与
与![]() 的解析式,并直接写出自变量
的解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com