
| A. | (5,-4) | B. | (-5,4) | C. | (5,-4)或(-5,4) | D. | (4,-5)或(-4,5) |
分析 作PQ⊥x轴于点Q,则OQ=45,PQ=5,于是把点旋转的问题转化为直角三角形旋转的问题,讨论:当把△OPQ绕原点逆时针旋转90°得到△OP′Q′,根据旋转的性质得P′Q′=PQ=5,OQ′=OQ=4,则P′(-5,4),当把△OPQ绕原点顺时针旋转90°得到△OP″Q″,同样方法易得P″(5,-4).
解答 解: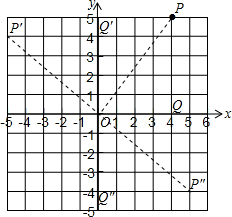 作PQ⊥x轴于点Q,则OQ=45,PQ=5,
作PQ⊥x轴于点Q,则OQ=45,PQ=5,
当把△OPQ绕原点逆时针旋转90°得到△OP′Q′,则P′Q′=PQ=5,OQ′=OQ=4,所以P′(-5,4),
当把△OPQ绕原点顺时针旋转90°得到△OP″Q″,同样方法可得P″(5,-4),
所以点P1的坐标是(-5,4)或(5,-4).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
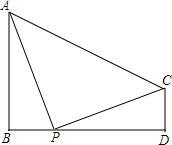 如图,已知AB丄BD,CD丄BD.
如图,已知AB丄BD,CD丄BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com