
【题目】我们知道,![]() 可以理解为
可以理解为![]() ,它表示:数轴上表示数
,它表示:数轴上表示数![]() 的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点
的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点![]() ,分别用数
,分别用数![]() 表示,那么
表示,那么![]() 两点之间的距离为
两点之间的距离为![]() ,反过来,式子
,反过来,式子![]() 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离.利用此结论,回答以下问题:
的点之间的距离.利用此结论,回答以下问题:
(1)数轴上表示数8的点和表示数3的点之间的距离是_________,数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离是__________.
的点之间的距离是__________.
(2)数轴上点![]() 用数
用数![]() 表示,若
表示,若![]() ,那么
,那么![]() 的值为_________.
的值为_________.
(3)数轴上点![]() 用数
用数![]() 表示:
表示:
①若![]() ,那么
,那么![]() 的值是________.
的值是________.
②当![]() 时,数
时,数![]() 的取值范围是________,这样的整数
的取值范围是________,这样的整数![]() 有________个.
有________个.
③![]() 有最小值,最小值是___________.
有最小值,最小值是___________.
【答案】(1)5;2;(2)5或![]() ;(3)①
;(3)①![]() 或8;②
或8;②![]() ,6;③2020.
,6;③2020.
【解析】
(1)根据两点之间的距离公式进一步计算即可;
(2)根据绝对值的定义求解即可;
(3)①利用绝对值的定义可知![]() 或
或![]() ,然后进一步计算即可;②
,然后进一步计算即可;②![]() 的意义是表示数轴上到表示
的意义是表示数轴上到表示![]() 和表示3的点的距离之和是5的点的坐标,据此进一步求解即可;③
和表示3的点的距离之和是5的点的坐标,据此进一步求解即可;③![]() 是表示数轴上表示3与表示
是表示数轴上表示3与表示![]() 的点的距离之和,然后进一步求解即可.
的点的距离之和,然后进一步求解即可.
(1)数轴上表示数8的点和表示数3的点之间的距离是:![]() ;
;
数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离是:
的点之间的距离是:![]() ,
,
故答案为:5,2;
(2)若![]() ,则
,则![]() 或
或![]() ,
,
故答案为:5或![]() ;
;
(3)①若![]() ,则
,则![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
故答案为:![]() 或8;
或8;
②∵![]() 的意义是表示数轴上到表示
的意义是表示数轴上到表示![]() 和表示3的点的距离之和是5的点的坐标,
和表示3的点的距离之和是5的点的坐标,
∴![]() ,其中整数有
,其中整数有![]() 、
、![]() 、0、1、2、3共6个,
、0、1、2、3共6个,
故答案为:![]() ,6;
,6;
③∵![]() 是表示数轴上表示3与表示
是表示数轴上表示3与表示![]() 的点的距离之和,
的点的距离之和,
∴当![]() 时,
时,![]() 有最小值,
有最小值,
此时最小值为:![]() ,
,
故答案为:2020.


科目:初中数学 来源: 题型:
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
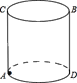
【题目】如图,圆柱的高为![]() ,底面半径为
,底面半径为![]() ,在圆柱下底面的
,在圆柱下底面的![]() 点处有一只蚂蚁,它想吃到上底面
点处有一只蚂蚁,它想吃到上底面![]() 处的食物,已知四边形
处的食物,已知四边形![]() 的边
的边![]() 、
、![]() 恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家喜欢玩的幻方游戏,老师精加创新改成了“幻圆”游戏,现在将-1,2,-3,4,5,6,- 7,8分别填入如图所示的四圈内,使横、整以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则![]() 的值为( )
的值为( )
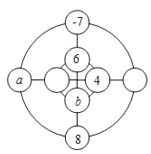
A.-8或1B.-1或1
C.-1或4D.-6或-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第![]() 个等式:
个等式:![]()
第![]() 个等式:
个等式:![]()
第![]() 个等式:
个等式:![]()
第![]() 个等式:
个等式:![]()
![]()
![]()
请回答下列问题:
(1)按以下规律列出第![]() 个等式:
个等式:![]() ______________
______________![]() ________________;
________________;
(2)用含![]() 的代数式表示第
的代数式表示第![]() 个等式:
个等式:![]() _______________
_______________![]() _______________(
_______________(![]() 为正整数)
为正整数)
(3)求![]() 的值.
的值.
(4)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
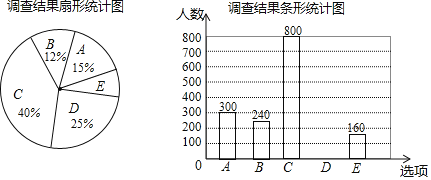
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com