
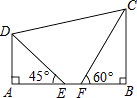
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
. 
(1)BC= .
(2)求点D到BC的距离.
(3)求DC的长.
【答案】
(1)3
(2)解:过点D作DG⊥BC于点G,
∵AD∥BC,AB⊥BC,
∴DG=AB,DA⊥AB,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BF=FCcos60°= ![]() ,
,
∴DC=AB=AE+EF+BF=2+2﹣ ![]() +
+ ![]() =4
=4
(3)解:∵DA⊥AB,∠AED=45°,
∴AD=AE=2,
∵DG⊥BC,AB⊥BC,
∴DG∥AB,
∵AD∥BC,
∴四边形ABGD是平行四边形,
∴BG=AD=2,
∴CG=BC﹣BG=3﹣2=1,
∴在Rt△DCG中,CD= ![]() =
= ![]() .
.
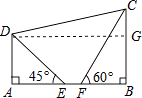
【解析】解:(1)∵AB⊥BC,
∴∠B=90°,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BC=FCsin60°=2 ![]() ×
× ![]() =3;
=3;
故答案为:3;
(1)由AB⊥BC,FC=2 ![]() °,∠BFC=60°,直接利用三角函数的知识求解即可求得答案;(2)首先过点D作DG⊥BC于点G,由AD∥BC,AB⊥BC,可得DG=AB,继而求得答案;(3)首先可得四边形ABGD是平行四边形,即可求得CG的长,然后由勾股定理求得答案.
°,∠BFC=60°,直接利用三角函数的知识求解即可求得答案;(2)首先过点D作DG⊥BC于点G,由AD∥BC,AB⊥BC,可得DG=AB,继而求得答案;(3)首先可得四边形ABGD是平行四边形,即可求得CG的长,然后由勾股定理求得答案.


科目:初中数学 来源: 题型:
【题目】已知等腰三角形的周长为20cm,底边长为ycm,腰长为xcm,y与x之间的函数表达式为y=20-2x,则自变量x的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=![]() CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).
①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
A.7200(1+x)2=8400B.7200(1+x2)=8400
C.7200(x2+x)=8400D.7200(1+x)=8400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( ) 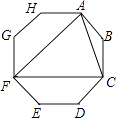
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是斜边
是斜边![]() 的中点,连接
的中点,连接![]() .
.
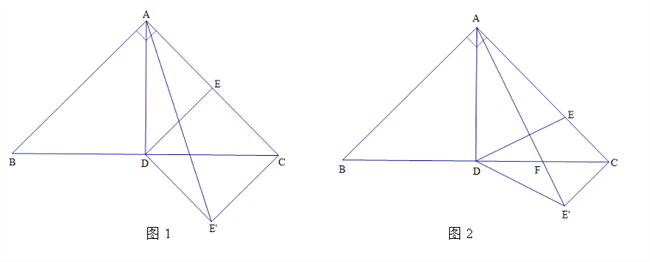
(1)如图1, ![]() 是
是![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)如图2,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com