
【题目】如图,在一个与地面垂直的截面中建立直角坐标系(横坐标表示地面位移,纵坐标表示高度),一架无人机的飞行路线为y=ax2+bx+c(a≠0),在直角坐标系中x轴上的线段AB上的某点起飞,途经空中线段EF上的某点,最后在线段CD上的某点降落,其中A(﹣2,0)、B(﹣1,0)、C(3,0)、D(4,0)、E(0,3)、F(0,2),则下列结论正确的有_____(填序号)
(1)abc<0;
(2)从起飞到当x≤1时无人机一直是上升的;
(3)2≤a+b+c≤4.5;
(4)最大飞行高度不超过4.
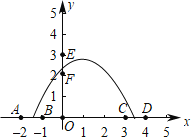
【答案】(1)(4)
【解析】
由抛物线的开口方向可判断a,由抛物线与y轴的交点可判断c,由对称性可得b的正负,进而可判断(1);
取起飞点A与降落点C,可得抛物线的对称轴,然后根据抛物线的性质可判断(2);
由图象可知,当抛物线过点B,点E,点C时,飞行高度最大,利用待定系数法求出此时的抛物线的解析式,从而可判断(3)(4)的正误.
解:∵由题意可知,抛物线开口向下,且抛物线的对称轴位于y轴右侧,
∴a<0,b>0,∵抛物线与y轴的交点在EF上,∴c>0,
∴abc<0,∴(1)正确;
当起飞点位于点A,而降落点位于点C时,对称轴为直线x=![]() <1,∴(2)不正确;
<1,∴(2)不正确;
由图象可知,当抛物线过点B,点E,点C时,飞行高度最大,
此时设y=a(x+1)(x﹣3),将E(0,3)代入得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3),
当x=1时,y=4,即最大飞行高度不超过4;故(4)正确,(3)不正确.
综上,(1)(4)正确.
故答案为:(1)(4).


科目:初中数学 来源: 题型:
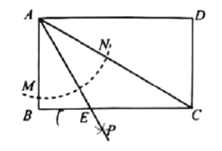
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式.
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求出
下方的抛物线上运动时,求出![]() 长度的最大值.
长度的最大值.
(3)当以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形时,求此时
为顶点的三角形是等腰三角形时,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象经过点
的图象经过点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
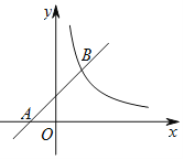
(1)求一次函数和反比例函数的表达式;
(2)设M是直线AB上一点,过M作MN∥x轴,交反比例函数![]() 的图象于点N,若以A,O,M,N为顶点的四边形是平行四边形,求点M的横坐标.
的图象于点N,若以A,O,M,N为顶点的四边形是平行四边形,求点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某公园里的一种健身器材,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
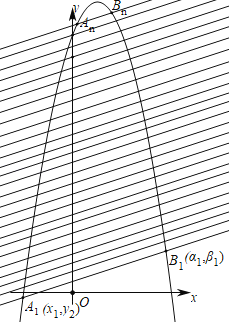
【题目】已知二次函数y=﹣x2+5x+2019,有一组平行直线与该函数的相交情况如下:
y1=2x+1与之交于A1(x1,y1)、B1(α1,β1),
y2=2x+2与之交于A2(x2,y2)、B1(α2,β2),
y3=2x+3与之交于A1(x3,y3)、B1(α3,β3),
……
yn=2x+n与之交于An(xn,yn)、Bn(αn,βn),
(1)求x1+α1与x2+α2的值;
(2)求整数n的最大值;
(3)求(x1+x1+x3+…+xn)+(α1+α2+α3+.…+αn)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
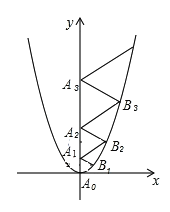
【题目】二次函数![]() 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2011在y轴的正半轴上,点B1,B2,B3,…,B2011在二次函数
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2011在y轴的正半轴上,点B1,B2,B3,…,B2011在二次函数![]() 位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2010B2011A2011都为等边三角形,则△A2010B2011A2011的边长=_____.
位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2010B2011A2011都为等边三角形,则△A2010B2011A2011的边长=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某科技物展览大厅有A、B两个入口,C、D、E三个出口.小昀任选一个入口进入展览大厅, 参观结束后任选一个出口离开.
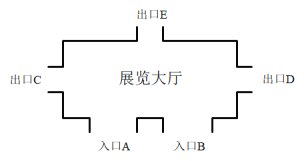
(1)若小昀已进入展览大厅,求他选择从出口C离开的概率.
(2)求小昀选择从入口A进入,从出口E离开的概率.(请用列表或画树状图求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com