
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式.
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求出
下方的抛物线上运动时,求出![]() 长度的最大值.
长度的最大值.
(3)当以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形时,求此时
为顶点的三角形是等腰三角形时,求此时![]() 的值.
的值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,线段
时,线段![]() 的长度有最大值,最大值为
的长度有最大值,最大值为![]() ;(3)
;(3)![]() 的值为6或
的值为6或![]() 或
或![]() 或3
或3
【解析】
(1)令![]() 即可得出点A的坐标,再根据点B的坐标利用待定系数法即可求得抛物线的解析式;
即可得出点A的坐标,再根据点B的坐标利用待定系数法即可求得抛物线的解析式;
(2)由点D的横坐标,可知点P和点D的坐标,再根据点![]() 在直线
在直线![]() 下方的抛物线上,即可表示PD解析式,并转化为顶点式就可得出答案;
下方的抛物线上,即可表示PD解析式,并转化为顶点式就可得出答案;
(3)根据题意分别表示出![]() ,
,![]() ,
,![]() 分当
分当![]() 时,当
时,当![]() 时,当
时,当![]() 时三种情况分别求出m的值即可.
时三种情况分别求出m的值即可.
(1)对于![]() ,取
,取![]() ,得
,得![]() ,∴
,∴![]() .
.
将![]() ,
,![]() 代入
代入![]() ,
,
得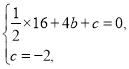 解得
解得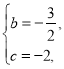
∴抛物线的解析式为![]() .
.
(2)∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 下方的抛物线上,
下方的抛物线上,
∴![]()
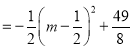 .
.
∵![]() ,
,
当![]() 时,线段
时,线段![]() 的长度有最大值,最大值为
的长度有最大值,最大值为![]() .
.
(3)由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]()
![]() ,
,![]() .
.
当![]() 为等腰三角形时,有三种情况:
为等腰三角形时,有三种情况:
①当![]() 时,
时,![]() ,即
,即![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ;
;
②当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ;
;
③当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() .
.
综上所述,![]() 的值为6或
的值为6或![]() 或
或![]() 或3.
或3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
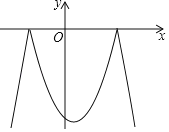
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2ax+m.
(1)当a=2,m=﹣5时,求抛物线的最值;
(2)当a=2时,若该抛物线与坐标轴有两个交点,把它沿y轴向上平移k个单位长度后,得到新的抛物线与x轴没有交点,请判断k的取值情况,并说明理由;
(3)当m=0时,平行于y轴的直线l分别与直线y=x﹣(a﹣1)和该抛物线交于P,Q两点.若平移直线l,可以使点P,Q都在x轴的下方,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
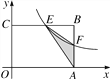
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某公司用800万元购得某种产品的生产技术后,进一步投入资金1550万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价需要定在200元到300元之间较为合理.销售单价![]() (元)与年销售量
(元)与年销售量![]() (万件)之间的变化可近似的看作是如下表所反应的一次函数:
(万件)之间的变化可近似的看作是如下表所反应的一次函数:
销售单价 | 200 | 230 | 250 |
年销售量 | 14 | 11 | 9 |
(1)请求出![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欢欢放学回家看到桌上有三个礼包,是爸爸送给欢欢和姐姐的礼物,其中![]() 礼包是芭比娃娃,
礼包是芭比娃娃,![]() 和
和![]() 礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
(1)欢欢随机地从桌上取出一个礼包,取出的是芭比娃娃的概率是多少?
(2)请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果,并求取出的两个礼包都是智能对话机器人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
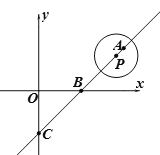
【题目】在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒![]() 个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
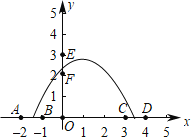
【题目】如图,在一个与地面垂直的截面中建立直角坐标系(横坐标表示地面位移,纵坐标表示高度),一架无人机的飞行路线为y=ax2+bx+c(a≠0),在直角坐标系中x轴上的线段AB上的某点起飞,途经空中线段EF上的某点,最后在线段CD上的某点降落,其中A(﹣2,0)、B(﹣1,0)、C(3,0)、D(4,0)、E(0,3)、F(0,2),则下列结论正确的有_____(填序号)
(1)abc<0;
(2)从起飞到当x≤1时无人机一直是上升的;
(3)2≤a+b+c≤4.5;
(4)最大飞行高度不超过4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com