
����Ŀ����ͼ����������ʻ�ڱ�ֱ�Ĺ�·�ϣ�����·����A��B��C��D�ĸ�վ�㣬ÿ������վ֮��ľ���Ϊ5ǧ�ף���Aվ����Dվ�ij���Ϊ���г�����Dվ����Aվ�ij���Ϊ���г�����һ�����г������г��ֱ��Aվ��Dվͬʱ������������У����Ժ����г������г�ÿ��10���ӷֱ���A��Dվͬʱ��һ����˿�ֻ�ܵ�վ���ϡ��³����ϡ��³���ʱ����Բ��ƣ������г������г����ٶȾ�Ϊ30ǧ��/Сʱ��
![]()
��1���ʵ�һ�����г���Bվ����һ�����г���Cվ�ֱ���ʱ���٣�
��2������һ�����г���ʻʱ��ΪtСʱ����һ�����г����һ�����г�֮��ľ���Ϊsǧ�ף���s��t�ĺ�����ϵʽ��
��3��һ�˿�ǰ��Aվ���£�����B��C��վ���P��������B��Cվ�����պ��������г���BP=xǧ�ף���ʱ���ӵ�֪ͨ��������35�����ڸϵ�������ѡ���ߵ�Bվ���ߵ�Cվ�����г�ǰ��Aվ�����˿͵IJ����ٶ���5ǧ��/Сʱ����x�����������
���𰸡���1��![]() ��
��![]() ����2����0��t��
����2����0��t��![]() ʱ��s=15��60t����
ʱ��s=15��60t����![]() ��t��
��t��![]() ʱ��s=60t��15����3��0��x��
ʱ��s=60t��15����3��0��x��![]() ��4��x��5��
��4��x��5��
��������
��1������ʱ��=·�̡��ٶ���ʽ������⣻
��2������t=![]() ʱ����һ�����г����һ�����г����������Է�0��t��
ʱ����һ�����г����һ�����г����������Է�0��t��![]() ��
��![]() ��t��
��t��![]() ����������ۼ��ɣ�
����������ۼ��ɣ�
��3���ɣ�2����֪ͬʱ������һ���ϡ����г���λ�ù���BC�е�Գƣ���˿͵���Aվ��ʱ��Ϊt���ӣ�����������������ۣ���x=2.5����x��2.5����x��2.5��
��1����һ�����г���Bվ��ʱ![]()
![]() Сʱ��
Сʱ��
��һ�����г���Cվ�ֱ���ʱ![]() Сʱ��
Сʱ��
��2����0��t��![]() ʱ��s=15��60t����
ʱ��s=15��60t����![]() ��t��
��t��![]() ʱ��s=60t��15��
ʱ��s=60t��15��
��3���ɣ�2����֪ͬʱ������һ���ϡ����г���λ�ù���BC�е�Գƣ���˿͵���Aվ��ʱ��Ϊt���ӣ�
�ٵ�x=2.5ʱ����Bվ��ʱ30���ӣ�����Ҫ�ٵ����г�5���ӣ�
t=30+5+10=45���������⣻
�ڵ�x��2.5ʱ��ֻ����Bվ�����г�������Bվxǧ�ף��������ұ���������г���CվҲ��xǧ�ף��������г���Bվ��5��x��ǧ�ף�
����ܳ����Ҳ�ĵ�һ�����г�����![]() ����ã�x��
����ã�x��![]() ��
��
��0��x��![]() ��
��
��18![]() ��t��20��
��t��20��
��0��x��![]() �������⣻
�������⣻
����˲����Ҳ��һ�����г���ֻ�ܳ��Ҳ�ڶ������г���x��![]() ��
��
![]() ����ã�x��
����ã�x��![]() ��
��
��![]() ��22
��22![]() ��t��28
��t��28![]() ��
��
��![]() �������⣻
�������⣻
����˲����Ҳ�ڶ������г���ֻ�ܳ��Ҳ���������г���x��![]() ��
��
![]() ����ã�x��
����ã�x��![]() ��
��
��![]() ��x��
��x��![]() ��35
��35![]() ��t��37
��t��37![]() ���������⣬
���������⣬
�����ϣ���0��x��![]() ��
��
�۵�x��2.5ʱ���˿�����Cվ�������г������������������г���Bվ�ǣ�5��x��ǧ�ף������ұ���������г���CվҲ�ǣ�5��x��ǧ�ף�
��������Ҳ��һ�����г�����![]() ����ã�x��5���������⣮
����ã�x��5���������⣮
��x��5���������⣮
����˲����Ҳ��һ�����г���ֻ�ܳ��Ҳ�ڶ������г���x��5��
![]() �����x��4��
�����x��4��
��4��x��5��30��t��32��
��4��x��5�������⣮
����˲����Ҳ�ڶ������г���ֻ�ܳ��Ҳ���������г���x��4��
![]() �����x��3��
�����x��3��
��3��x��4��42��t��44��
��3��x��4�������⣮
���ϣ���4��x��5��
����������0��x��![]() ��4��x��5��
��4��x��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
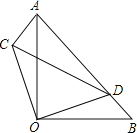
����Ŀ����ͼ����AOB����COD�ǵ���ֱ�������Σ���D��AB�ϣ�
��1����֤����ACO�ա�BDO��
��2������BOD��30�㣬���ACD������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB��N����BC���ӳ�����M����A=40��.

�����NMB�Ĵ�С��
������ͼ�еġ�A�Ķ�����Ϊ70���������������䣬���NMB= ��
���㷢����ʲô���Ĺ��ɣ�������A��Ϊ�۽ǣ��������������Ե���ʶ�Ƿ���Ҫ�����ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���μ�ѡ���߰������ѧУ�о�С�������ȡ�����˽��е�������������ռ����������ݻ��Ƴɲ�����������ͳ��ͼ������ͳ��ͼ���γ����������£�
A����ѧ��γ� B��������γ� C��������γ�
����������Ϣ������������⣺
��1����С����õĵ��鷽ʽ���� ����������������������� ����
��2��������ͳ��ͼ������ͳ��ͼ����������
��3����ȫУ��1280��ѧ����ѡ��������γ̵�ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬AC=BC=10������DCE�У���DCE=90�㣬DC=EC=6����D���߶�AC�ϣ���E���߶�BC���ӳ����ϣ�����DCE�Ƶ�C��ת60���õ���D��CE������D�Ķ�Ӧ��Ϊ��D������E�Ķ�Ӧ��Ϊ��E����������AD�䡢BE��������C��CN��BE��������ΪN��ֱ��CN���߶�AD���ڵ�M����MN�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��a��0������E��10��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ߣ�����C��D���������ϣ���A��t��0������t=2ʱ��AD=4��
��1���������ߵĺ�������ʽ��
��2����tΪ��ֵʱ������ABCD���ܳ������ֵ�����ֵ�Ƕ��٣�
��3������t=2ʱ�ľ���ABCD����������ƽ�������ߣ���ƽ�ƺ������������εı�����������G��H����ֱ��GHƽ�־��ε����ʱ����������ƽ�Ƶľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A������ B��ƹ����C����ë�� D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺


��1����α������ѧ�������� ���ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ���DΪ AC����һ�㣬��BDΪ�����ȱ���BDE�� ����CE����CD��1��CE��3����BC��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸�����������ˮ�ʣ�����������ij�����۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�������
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
������ˮ������/�£� | 220 | 180 |
�����飺����һ̨A���豸�ȹ���һ̨B���豸��3��Ԫ������2̨A���豸�ȹ���3̨B���豸��3��Ԫ��
��1����a��b��ֵ��
��2����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���100��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���ʵ������£���ÿ��Ҫ��������ˮ��������1880�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com