
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于M,∠A=40°.

⑴求∠NMB的大小;
⑵若将图中的∠A的度数改为70°,其余条件不变,则∠NMB= ;
⑶你发现有什么样的规律?若将∠A改为钝角,对这个问题规律性的认识是否需要加以修改?
【答案】(1)20°;(2)35°;(3)规律为:在等腰△ABC中,当AB=AC,∠A是锐角时,∠NMB的度数恰好为顶角∠A度数的一半;当∠A为钝角时,上述规律依然成立,不需要修改.
【解析】
(1)在等腰三角形ABC中可求出∠B,然后在△BMN中根据内角和求解;
(2)解法同(1);
(3)依照(1)(2)的解法,找出∠NMB与∠A的关系,当∠A为钝角时,作出图形,根据三角形内角和定理进行证明.
解:(1)∵AB=AC
∴∠B=∠ACB
∴![]()
∵MN⊥AB,
∴∠MNB=90°,
∴∠NMB=90°-∠B=90°-70°=20°
(2)当∠A=70°时,如下图所示,
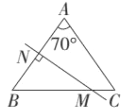
∵AB=AC
∴∠B=∠ACB
∴![]()
∵MN⊥AB,
∴∠MNB=90°,
∴∠NMB=90°-∠B=90°-55°=35°
(3)如图,规律为:在等腰△ABC中,当AB=AC,∠A是锐角时,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.
∠A.

证明: ∵AB=AC
∴∠B=∠ACB
∴![]()
∵MN⊥AB,
∴∠MNB=90°,
∴![]()
即∠NMB的大小等于顶角∠A的一半.
当∠A为钝角时,上述规律依然成立,故不需要修改. 完整地叙述上述规律为:等腰三角形一腰上的垂直平分线与底边或底边的延长线相交,所成的锐角等于顶角的一半.
证明:如图,
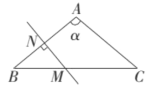
∵AB=AC
∴∠B=∠ACB
∴![]()
∵MN⊥AB,
∴∠MNB=90°,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图是在写字台上放置一本摊开的数学书和一个折叠式台灯时的截面示意图,已知摊开的数学书AB长20cm,台灯上半节DE长40cm,下半节DC长50cm.当台灯灯泡E恰好在数学书AB的中点O的正上方时,台灯上、下半节的夹角即∠EDC=120°,下半节DC与写字台FG的夹角即∠DCG=75°,求BC的长.(书的厚度和台灯底座的宽度、高度都忽略不计,F、A、O、B、C、G在同一条直线上.参考数据:sin75°≈0.97,cos75°≈0.26,![]() ≈1.41,结果精确到0.1)
≈1.41,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王某月手机话费中的各项费用统计情况如图表所示,请你根据图表信息完成下列各题
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 4.8 | 48 |
|
|

(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB和△APQ都是等边三角形.
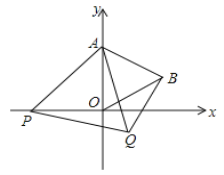

⑴求点B的坐标;
⑵试判断直线AB与直线BQ的位置关系,并证明;
⑶连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,延长AC到E,C为线段AE上的一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC. 以下五个结论:①AD=BE;②AP=BO;③PQ//AE;④∠AOB=60°;⑤OC平分∠AOE;结论正确的有_________(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公交车行驶在笔直的公路上,这条路上有A,B,C,D四个站点,每相邻两站之间的距离为5千米,从A站开往D站的车称为上行车,从D站开往A站的车称为下行车,第一班上行车、下行车分别从A站、D站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在A,D站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
![]()
(1)问第一班上行车到B站、第一班下行车到C站分别用时多少?
(2)若第一班上行车行驶时间为t小时,第一班上行车与第一班下行车之间的距离为s千米,求s与t的函数关系式;
(3)一乘客前往A站办事,他在B,C两站间的P处(不含B,C站),刚好遇到上行车,BP=x千米,此时,接到通知,必须在35分钟内赶到,他可选择走到B站或走到C站乘下行车前往A站.若乘客的步行速度是5千米/小时,求x满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠BAC=90°,AB=AC,BM是AC边的中线,作AD⊥BM,垂足为点E,交BC于点D,且AH平分∠BAC交BM于N,交BC于H,连接DM,则下列结论:①∠AMB=∠CMD②HN=HD③BN=AD④∠BNH=∠MDC⑤MC=DC中,正确的有( )个

A.5个B.4个C.3个D.2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com