
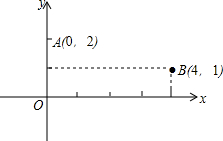
 已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标. 分析 先求得直线BC的解析式,然后利用一次函数与坐标轴交点求法得出答案即可.
解答 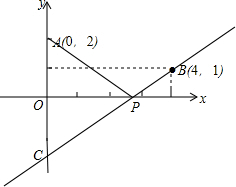 解:∵A(0,2),
解:∵A(0,2),
∴A点关于x轴对称点C坐标为;(0,-2),
连接A′B交x轴于点P,
由题意得;A′(0,-2),
将A′(0,-2),B(4,1)代入y=kx+b得:$\left\{\begin{array}{l}{b=-2}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-2}\end{array}\right.$,
∴直线A′B的解析式为:y=$\frac{3}{4}$x-2,
∴y=0时,x=$\frac{8}{3}$,
∴P($\frac{8}{3}$,0).
点评 此题主要考查了最短路径求法以及待定系数法求一次函数解析式等知识,求得直线BC的解析式是解题关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
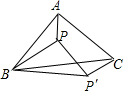 如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.
如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
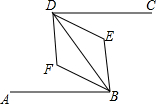 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )| A. | ∠ABE=2∠CDE | B. | ∠ABE=3∠CDE | C. | ∠ABE=∠CDE+90° | D. | ∠ABE+∠CDE=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com