
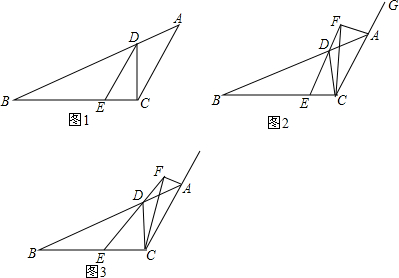
分析 (1)由三角形外角的性质得出∠BDC=∠ACD+∠DAC=2∠DAC,角平分线的性质得出∠BDE=∠BAC,得出结论;
(2)①②类比(1)的方法利用三角形外角的性质和三角形的内角和得出答案即可.
解答 解:(1)∵∠ACD=∠DAC且∠BDC=∠ACD+∠DAC,
∴∠BDC=2∠DAC,
∵DE平分∠BDC,
∴∠BDE=∠BAC,
∴DE∥AC.
(2)∵∠BAG=∠ADC+∠ACD,
∴$\frac{1}{3}$∠BAG=$\frac{1}{3}$∠ADC+$\frac{1}{3}$∠ACD,
∴∠FAG=∠FCA+$\frac{2}{3}$∠ADC且∠FAG=∠FCA+∠AFC,
∴∠AFC=80°.
(3)设∠DAC=X=∠DCA,
∴∠BDC=2X,∠BAG=180°-X,
∴∠BDE=∠FDA=$\frac{2X}{3}$,∠DAF=60°-$\frac{X}{3}$,
∴∠DFA=120°-$\frac{X}{3}$,
∴∠DFA+$\frac{1}{3}$∠DAC=120°
点评 此题考查三角形的内角和定理,外角的性质,以及角平分线的性质,综合利用基础知识解决问题.


科目:初中数学 来源: 题型:解答题
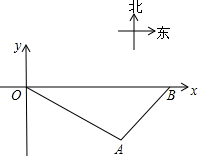 一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.
一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -7 | B. | 3 | C. | 7 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com