
分析 (1)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入-经营总成本=wA+wB-3×20;
②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类草梅的数量;
(2)本问是方案设计问题,总投入为100万元,这笔100万元包括购买草莓的费用+A类草梅加工成本+B类草莓加工成本.共购买了m吨草莓,其中A类草莓为x吨,B类草莓为(m-x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.
解答 解:(1)①设销售A类草莓x吨,则销售B类草莓(20-x)吨.
①当2≤x<8时,
wA=x(-x+14)-x=-x2+13x;
wB=9(20-x)-[12+3(20-x)]=108-6x
∴w=wA+wB-3×20
=(-x2+13x)+(108-6x)-60
=-x2+7x+48;
当x≥8时,
wA=6x-x=5x;
wB=9(20-x)-[12+3(20-x)]=108-6x
∴w=wA+wB-3×20
=(5x)+(108-6x)-60
=-x+48.
∴w关于x的函数关系式为:
w=$\left\{\begin{array}{l}{-{x}^{2}+7x+48(2≤x<8)}\\{-x+48(x≥8)}\end{array}\right.$.
②当2≤x<8时,-x2+7x+48=30,解得x1=9,x2=-2,均不合题意;
当x≥8时,-x+48=30,解得x=18.
∴当毛利润达到30万元时,直接销售的A类草莓有18吨.
(2)设投入资金后甲类分到收购的草莓为x吨,乙类为y吨,
总投入为3(x+y)+x+12+3y=100,
即:2x+3y=44,
当x<8时总利润为w=(-x+14)x+9×$\frac{44-2x}{3}$-100=-x2+8x+32=-(x-4)2+48,
当x=4时,取到最大值48;
当x≥8时,总利润w=6x+9×$\frac{44-2x}{3}$-100=32为常数,
故方案为收购16吨,甲类分配4吨,乙类分配12吨,总收益为48万元.
点评 本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
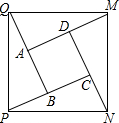 如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.
如图,将正方形ABCD的四边各延长一倍.即DM=AD,CN=CD,AQ=AB,BP=BC.连接M,N,P,Q四点,试判断MNPQ的形状,并予以证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 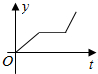 | B. | 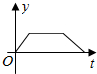 | C. | 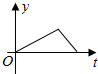 | D. | 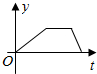 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com