
【题目】如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
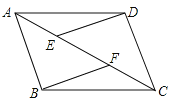
【答案】(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,AD=CB,AB∥CD,AD∥CB,进一步得到∠BAF=∠DCE,∠DAE=∠BCF,由SSS证明△ABC≌△CDA;由SAS证明△ABF≌△CDE;由SAS证明△ADE≌△CBF(SAS);
(2)由△ABF≌△△CDE,得出∠AFB=∠CED,即可证出DE∥BF.
试题解析:(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴∠BAF=∠DCE,∠DAE=∠BCF,在△ABC和△CDA中,∵AB=CD,CB=AD,AC=CA,∴△ABC≌△CDA(SSS);
∵AE=CF,∴AF=CE,在△ABF和△CDE中,∵AB=CD,∠BAF=∠DCE,AF=CE,∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF(SAS).
(2)∵△ABF≌△△CDE,∴∠AFB=∠CED,∴DE∥BF.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,
(1)请画出平移后的图形△A′B′C′;
(2)并写出△A′B′C′各顶点的坐标;
(3)求出△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点(﹣1,y1),(2,y2),(3,y3)是抛物线y=﹣x2+a上的三点,则y1、y2、y3的大小关系为( )
A.y3>y2>y1B.y1>y3>y2C.y3>y1>y2D.y1>y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB,CD内部一点,AB∥CD,连接EA,ED.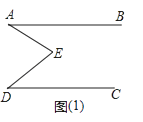
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)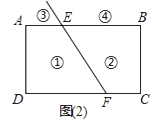
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com