Question

1．在平面直角坐标系中，已知A（0，a），B（b，0）（a＞0，b＜0），点P为△ABO的角平分线的交点．
（1）连接OP，a=4，b=-3，则OP=$\sqrt{2}$；（直接写出答案）
（2）如图1，连接OP，若a=-b，求证：OP+OB=AB；
（3）如图2，过点作PM⊥PA交x轴于M，若a²+b²=36，求AO-OM的最大值．

Answer 1

分析 （1）如图1中，作PE⊥OA，PF⊥B，PH⊥AB垂足分别为E、F、H，首先证明PH=PE=PF，其次证明四边形PEOF是正方形，推出OE=$\frac{OA+OB-AB}{2}$即可解决问题．
（2）如图3中，连接AP、BP，在x轴的正半轴上截取OM=OP，连接PM，证明△ABP≌△MBP即可．
（3）因为AO-MO=（AF+OF）-（EM-OE）=2OE，OE=$\frac{AO+BO-AB}{2}$，又因为（a+b）²=a²+b²+2ab≤2（a²+b²）≤72，所以a+b≤6$\sqrt{2}$由此即可解决问题．

解答 解：（1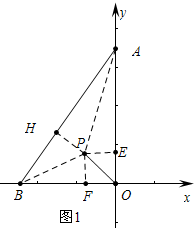）如图1中，作PE⊥OA，PF⊥B，PH⊥AB垂足分别为E、F、H．
在RT△AOB中，∵OA=4，OB=3，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
在△APE或△APH中，
$\left\{\begin{array}{l}{∠PHA=∠PEA}\\{∠PAH=∠PAE}\\{PA=PA}\end{array}\right.$，
∴△APH≌△APE，
∴AH=AE，PH=PE，同理BH=BF，PH=PF，
∵∴PE=PH=PF，
∵∠PFO=∠PEO=∠EOF=90°，
∴四边形PEOF是矩形，∵PE=PF，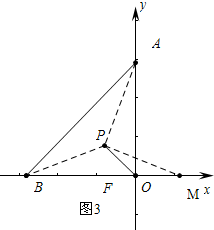
∴四边形PEOF是正方形，
∴PE=PF=OF=OE，
∴OA+OB-AB=AE+OE+BF+OF-AH-BH=2EO，
∴EO=$\frac{OA+OB-AB}{2}$=1，
∴OP=$\sqrt{P{E}^{2}+O{E}^{2}}$=$\sqrt{2}$，
故答案为$\sqrt{2}$．
（2）如图3中，连接AP、BP，在x轴的正半轴上截取OM=OP，连接PM，
则∠OMP=∠OPM=$\frac{1}{2}$∠POB，
∵P为△AOB角平分线交点，∠AOB=90°，OA=OB，
∴∠BAO=∠AOP=∠BOP=∠ABO=45°，
∴∠ABP=∠MBP，∠PMO=∠OAP=∠BAP=$\frac{1}{2}$×45°=22.5°，
在△ABP和△MBP中，
$\left\{\begin{array}{l}{∠BAP=∠BMP}\\{∠ABP=∠MBP}\\{BP=BP}\end{array}\right.$，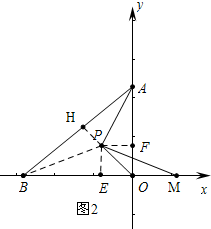
∴△ABP≌△MBP（AAS），
∴AB=BM=OB+OP．
（3）在图2中，作PE⊥x轴于E，PF⊥y轴于点F，PH⊥AB于H，
则∠AFP=∠MEP=90°，
∵∠AFP=∠MEP=90°，
∵P是△AOB的角平分线交点，
∴PF=PE，
∵PE⊥x轴，PF⊥y轴，
∴∠PFO=∠PEO=90°，
∴∠FPE=90°，
∵AP⊥PM
∴∠APM=90°=∠FPE，
∴∠APM-∠FPM=∠FPE-∠FPM，
即：∠APF=∠MPE，
在△APF和△MPE中，
$\left\{\begin{array}{l}{∠APF=∠MPE}\\{PF=PE}\\{∠PFA=∠PEM}\end{array}\right.$，
∴△APF≌△MPE，
∴AF=EM，
∴AO-MO=（AF+OF）-（EM-OE）=2OE，
∵a²+b²=36，AB=6，OE=$\frac{AO+BO-AB}{2}$，
∵（a+b）²=a²+b²+2ab≤2（a²+b²）≤72在
∴a+b≤6$\sqrt{2}$
∴OE的最大值为3$\sqrt{2}$-3，
∴AO-OM的最大值为6$\sqrt{2}$-6．

点评 本题考查全等三角形的判定和性质、勾股定理、直角三角形的内切圆的半径的求法等知识，这里的难点是用到不等式的性质：a²+b²≥2ab，解题的关键是利用全等三角形解决问题．